Вследствие конечной длительности пребывания системы в возбужденном состоянии, люминесценция не исчезает мгновенно после прекращения возбуждения, а затухает с определенной скоростью. В случае внутрицентровой люминесценции излучательный переход в каждом центре происходит независимо от состояния других центров и определяется только его вероятностью.
Если N – число возбужденных центров свечения в момент времени t, а t – среднее время «жизни» возбужденного состояния, то число центров dN, переходящих в основное состояние за время dt, будет равно
dN = -N
.
(1)
Преобразуя выражение (1) и интегрируя, получим
lnN = -
+ const.
(2)
Если в начале процесса (при t = 0) N = N0, то
N = N0
.
(3)
Интенсивность свечения I определяется числом излучательных переходов в единицу времени (для простоты будем считать её равной этому числу, хотя в целом это – энергетическая характеристика излучения):
I = -
=
= 
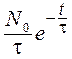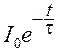. (4)
Таким образом, приходим к экспоненциальному закону затухания внутрицентровой люминесценции.
В случае рекомбинационной люминесценции интенсивность свечения пропорциональна скорости рекомбинации электронов с ионизированными центрами, а эта скорость определяется числом эффективных встреч между ними. Можно считать, что это число пропорционально произведению концентраций участников процесса – ионизированных центров свечения NA и свободных электронов п:
I = -
= bNAn,
(5)
где b – коэффициент рекомбинации.
Если концентрацией электронов в отсутствие возбуждения пренебречь, то NA = п и
I = -
= bn2.
(6)
Разделяя переменные и интегрируя, найдем
= bt + const.
(7)
Если при t = 0 имеем п = n0, то
n =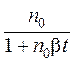
.
(8)
Подставляя последнее выражение в (6), получим
I =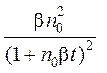 
. (9)
При t = 0
I = I0 = bn02; n0 =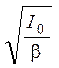 
.
Окончательно получаем
I =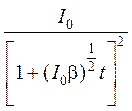 
. (10)
Закон затухания рекомбинационной люминесценции при сделанных предположениях выражается уравнением гиперболы второго порядка. Это уравнение для экспериментальной проверки удобно преобразовать, придав ему следующий вид:
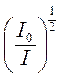- 1 = (I0b)½t, (11)
отсюда в координатах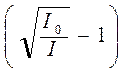 
и t графиком функции должна получиться прямая линия.
Рассмотренные два основных типа люминесценции отличаются друг от друга также по зависимости затухания от интенсивности возбуждения. Как следует из выражений (4) и (11), при внутрицентровой люминесценции относительное изменение интенсивности свечения при затухании не зависит от I0, а следовательно, и от интенсивности возбуждения, тогда как при рекомбинационной люминесценции это изменение тем быстрее, чем больше I0. Поэтому слабое возбуждение люминесценции невыгодно в тех случаях, когда рекомбинационное послесвечение создает помехи, например, при наблюдении на экране движущихся предметов.
Из уравнения (10) следует, что при достаточно большом t интенсивность рекомбинационного послесвечения не зависит от начальной интенсивности. Кривые затухания, полученные после возбуждения люминофора излучениями различной интенсивности, будут асимптотически приближаться друг к другу.
Кроме центров свечения, в люминофоре могут находиться примесные центры, которые имеют свободный локальный уровень вблизи дна зоны проводимости. Эти центры могут захватывать электрон из зоны проводимости (см. рис. 1, переход 13) и удерживать его в течение длительного времени. Переход захваченного электрона в валентную зону для таких центров маловероятен, но существует вероятность обратного переброса электрона в зону проводимости (переход 14), где он в конечном итоге может принять участие в процессах рекомбинации. Такие центры, образующие метастабильные состояния в запрещенной зоне, называются электронными ловушками (центрами захвата). Возможно образование в кристалле и дырочных ловушек. Наличие таких ловушек обусловливает длительное затухание люминесценции кристаллов после прекращения их возбуждения. В этом случае для описания затухания люминесценции следует заменить вышеприведенные дифференциальные уравнения системой дифференциальных уравнений, содержащих несколько переменных, учитывающих захват электронов на ловушки.
Анализ этой системы показывает, что если ловушки расположены по соседству с центрами свечения и если возбужденные электроны пробегают очень малые расстояния (меньше 10-6 см), перемещаясь лишь от ловушки до центра свечения или наоборот, то такую систему можно рассматривать как независимую. В этом случае вероятность рекомбинации постоянна во времени, и затухание будет следовать экспоненциальному закону (в данной ситуации время t соответствует пребыванию электрона в ловушке).
Если ловушки распределены в пространстве независимо от центров свечения и пробег электрона достаточно велик, чтобы позволить ему рекомбинировать с большим числом центров (пробег больше 10-5 см), то вероятность рекомбинации будет пропорциональна числу ионизированных центров. Мы опять получаем для кинетики затухания уравнение гиперболы второго порядка. Скорость затухания при этом будет определяться, в основном, временем пребывания электронов на ловушках.
Таким образом, затухание по гиперболе второго порядка однозначно устанавливает, что люминесценция является рекомбинационной. Часто ситуация существенно усложняется из-за вклада в кинетику затухания ловушек различного типа, отличающихся друг от друга глубиной. Тем не менее, математический анализ процесса показывает, что и в этом случае затухание рекомбинационной люминесценции подчиняется гиперболическому закону, но с показателем степени 1 £ p £ 2.
Это приводит к уравнению гиперболы дробной степени
I =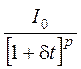 
,
(13)
впервые эмпирически полученному Э. Беккерелем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.