Методические указания к лабораторным работам "Изучение свободных колебаний связанной системы тел", "Изучение релаксационных электрических колебаний", "Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа", "Вынужденные колебания в последовательном электрическом контуре", страница 5

№ п/п	R, Oм	С, Ф	UП, В	tР, с	tЗ, с	Т, с	Т, с
1
2
3
4

Сравните t_Р и t_З. Определите период релаксационных колебаний по формуле (5) и внесите его значения в табл. 3.

III. Обработка результатов измерений

Оцените погрешность определения периода релаксационных колебаний по косвенным измерениям.

Для этого определите относительную ошибку косвенных измерений dТ, используя формулу (6):

dT =  +  +  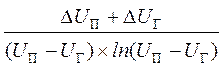+ 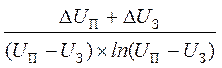,  (6)

где DR, DC, DU_П, DU_Г и DU_З – максимальные значения приборных ошибок. Затем определите предельную абсолютную ошибку косвенных измерений по формуле:

DТ = Т ´ dТ.                                           (7)

Округлите результаты вычислений и полученные данные занесите в табл. 3.

ЗАДАНИЕ ДЛЯ УИРС

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ПЕРИОДА РЕЛАКСАЦИОННЫХ КОЛЕБАНИЙ

ОТ ПАРАМЕТРОВ КОНТУРА

Приборы и принадлежности. Неоновая лампа, выпрямитель, потенциометр, осциллограф, звуковой генератор, конденсаторы, сопротивления.

Порядок выполнения работы

1. Соберите схему, изображенную на рис. 2.

2. С помощью переключателя П₁ подключите к Х-входу осциллографа неоновую лампу. Получите на экране осциллографа устойчивую неподвижную картину релаксационных колебаний при определенных значениях R и С, подбирая напряжение на неоновой лампе потенциометром П и изменяя частоту развертки осциллографа.

Подсчитайте число циклов разрывных колебаний п. Данные занесите в табл. 4.

Таблица 4

№	R, Oм	С, Ф	n	νЗГ, Гц	ТЭ, с	Т, с
1
2
3
4

3. Подключите с помощью переключателя П₁ к Y-входу осциллографа звуковой генератор ЗГ вместо неоновой лампы. Плавно изменяя частоту звукового генератора, добейтесь на экране осциллографа стабильной осциллограммы, такой, чтобы число циклов синусоидальных колебаний от звукового генератора равнялось числу циклов разрывных колебаний при частоте развертки осциллографа, применяемой при измерениях в п. 2. Зафиксируйте частоту звукового генератора (которая равна частоте исследуемых разрывных колебаний). Данные занесите в табл. 4.

4. Повторите измерения, указанные в п.п. 2, 3, для других комбинаций R и С.

Вычислите период релаксационных колебаний по формуле (5) и формуле

Т_Э = 1/n_ЗГ.                                             (8)

В первом случае проведите обработку результатов измерений, рассчитав относительную ошибку косвенных измерений, приводимую выше без вывода (см. формулу (6)). Полученные данные занести в табл. 4.

5. Сравните периоды релаксационных колебаний, вычисленные по формулам (5) и (8). Объясните причину расхождения результатов расчётов.

Контрольные вопросы

1. Каковы особенности автоколебаний?

2. В чем заключается различие автоколебаний и вынужденных колебаний?

3. Чем отличаются механизмы процессов образования релаксационных и почти гармонических колебаний?

4. Каким образом можно осуществить наблюдение релаксационных колебаний на экране осциллографа?

5. Выведите формулу для вычисления периода релаксационных колебаний.

6. Назовите практические применения релаксационных колебаний.

7. Каким образом можно экспериментально определить период релаксационных колебаний?

Список литературы

1.  Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

2.  Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 29

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.

Приборы и принадлежности: панель с колебательным контуром, магазин сопротивлений, электронный осциллограф, соединительные провода.

Введение

На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор электроёмкостью C, катушку индуктивностью L и резистор с активным сопротивлением R.

Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Исследуем характер колебаний, возникающих в идеализированном колебательном контуре в отсутствие сопротивления R = 0 при сообщении конденсатору заряда q₀.

Вначале энергия электрического поля конденсатора емкостью Cравна:

W_C = q₀²/2C =CU₀²/2,

где U₀ = q₀/С - максимальнаяразность потенциалов на обкладках конденсатора. Под действием электрического поля начинается движение зарядов и конденсатор разряжается. В контуре возникает электрический ток:

I(t) = – dq(t)/dt,                                        (1)

где dq(t) – изменение заряда на обкладках конденсатора. Знак минус показывает, что возникновение тока сопровождается уменьшением заряда на обкладках конденсатора (dq < 0).