Физика \ Физика

Методические указания к лабораторным работам "Изучение свободных колебаний связанной системы тел", "Изучение релаксационных электрических колебаний", "Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа", "Вынужденные колебания в последовательном электрическом контуре", страница 13

Пользуясь калибровочной сеткой экрана осциллографа, измерьте величины первых четырех последовательно расположенных (через период) амплитуд колебаний U01, U02, U03, U04 (см. рис. 4). Данные измерений занесите в таблицу 1.

Таблица 1

№

RМ,Ом

U01

U02

U03

U04

1

1

2

100

3

200

Повторите измерения, выставив на магазине сопротивлений сначала 100 Ом, а затем 200 Ом. Для этого на верхней клавишной панели нажимается кнопка 102, а на нижней – в первом случае – кнопка 1, а во втором – кнопка 2. Данные измерений занесите в таблицу 1.

Увеличивая сопротивление магазина RМ, наблюдайте увеличение затухания и определите сопротивление RКР, при котором полностью прекращается колебательный процесс – процесс становится апериодическим (рис. 2в). Запишите значение этого сопротивления.

Выключите тумблеры «Сеть» на функциональном генераторе и осциллографе, а также отожмите кнопки на клавишных панелях магазина сопротивлений. Выключите питание на щите установки.

Обработка результатов измерений

Рассчитайте для каждого сопротивления RМ величины логарифмического декремента d1, d2, d3, по формуле dI = ln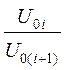(см. формулу 14), а потом и dСР. Используя формулу (12), определите значения добротностей Q1, Q2, Q3 и среднее арифметическое значение добротности . Результаты запишите в таблицу 2.

Таблица 2

№

RМ, Ом

d1

d2

d3

dСР

Q1

Q2

Q3

R = RМ + RЦ, Ом

QТ

1

1

2

100

3

200

Постройте график зависимости dСР от RМ и по графику (продолжая прямую до пересечения с осью абсцисс) найдите сопротивление цепи RЦ(рис. 5), а затем и общее сопротивление R = RМ + RЦ. Результаты вычислений запишите в таблицу 2.

Рассчитайте для заданных значений L и C (они приведены на установке) теоретические значения добротностей QТ =  = 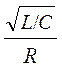. Результаты запишите в таблицу 2 и сравните со значениями .

Рассчитайте теоретическое значение критического сопротивления RКР = 2 и сравните его с экспериментально полученным ранее.

Рассчитайте погрешности измерений добротности контура для одного из сопротивлений RМ. Среднее арифметическое значение добротности контура определяется по формуле

=.

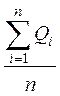где п –число полученных значений добротности (Q1, Q2,Q3),

Абсолютную погрешность оцените по формуле:

 = .

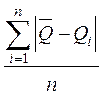Округлите величину  в соответствие с теорией ошибок [3].

Вычислите относительную погрешность измерений:

dQ = ×100 %.

Oкруглите величину  в соответствии с полученной абсолютной погрешностью . Окончательный результат запишите в виде:

Q = +.

Контрольные вопросы

1. Чем отличается реальный колебательный контур от идеализированного?

2. Как происходит возбуждение колебаний в исследуемом контуре?

3. Дайте определение свободных незатухающих электромагнитных колебаний, затухающих электромагнитных колебаний.

4. Напишите дифференциальное уравнение колебаний для контура и его решение для случая b < w0.

5. Для каких физических величин в исследуемом контуре могут наблюдаться колебательные процессы? Укажите закон изменения этих величин во времени.

6. Объясните причины затухания колебаний в исследуемом контуре.

7. Покажите, как изменяется характер колебаний, если сопротивлением контура: а) пренебречь; б) сделать больше критического значения?

8. Назовите величины, характеризующие затухание колебаний, укажите их физический смысл и размерности.

9. Укажите зависимость логарифмического декремента, коэффициента затухания колебаний и добротности от электрических параметров контура.

10. Как изменится период затухающих колебаний, если: а) пренебречь активным сопротивлением контура; б) сделать его больше критического?

11. В течение какого времени амплитуда затухающих колебаний уменьшится: а) до половины максимального значения; б) в е раз?

Список литературы

1.  Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

2.  Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 130

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ПОСЛЕДОВАТЕЛЬНОМ

ЭЛЕКТРИЧЕСКОМ КОНТУРЕ

Цель работы: изучение вынужденных колебаний в последовательном электрическом контуре, определение добротности контура и индуктивности контура.

Приборы и принадлежности: колебательный контур, генератор синусоидальных колебаний, электронный осциллограф, соединительные провода.

Введение

Вынужденные электромагнитные колебания в электрическом контуре, содержащем емкость C, индуктивность L и активное сопротивление R (рис. 1), можно вызвать, если включить последовательно с элементами контура источник тока, э. д. с. которого изменяется по гармоническому закону

E= E0cosWt.                                          (1)

Для получения дифференциального уравнения, описывающего вынужденные колебания, запишем для этого контура закон Ома:

IR + U = E - L,                                     (2)

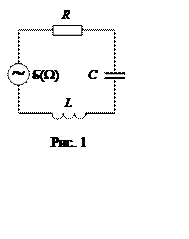
где U – напряжение на конденсаторе.

Поскольку U=q/C, получаем:

I =  = C;          =C.

Подставим эти выражения в уравнение (2):

LC + CR + U = E0cosWt.

Разделив обе части полученного равенства на LC и введя обозначения b =  и w02 = , получим дифференциальное уравнение вынужденных электромагнитных колебаний:

Скачать файл