Физика \ Физика

Методические указания к лабораторным работам "Изучение свободных колебаний связанной системы тел", "Изучение релаксационных электрических колебаний", "Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа", "Вынужденные колебания в последовательном электрическом контуре", страница 10

Для выполнения работы используется простейший колебательный контур, состоящий из последовательно соединенных катушки индуктивности L, конденсатора C и сопротивления R. Резонансные кривые снимают при различных сопротивлениях, включенных в контур. Наблюдение за изменением амплитуды колебаний на конденсаторе производится с помощью электронного осциллографа. Для этого сигнал с конденсатора подается на вход «Y» осциллографа, и при изменении частоты генератора измеряется амплитуда напряжения. При этом диапазон частот выбирается достаточно широким в обе стороны по отношению к резонансной частоте. Резонансная частота соответствует наибольшей амплитуде измеряемого напряжения при заданном сопротивлении контура. Определение добротности контура производится двумя из вышеописанных способов: по ширине резонансной кривой и по отношению резонансного напряжения к амплитуде вынуждающей э. д. с. Полученные результаты позволяют вычислить омическое сопротивление контура и оценить значение внутреннего сопротивления генератора.

Порядок выполнения работы

1. Включите генератор синусоидальных колебаний и электронный осциллограф и соберите схему для измерений в соответствии с указаниями на стенде.

2. Рассчитайте собственную частоту контура по формуле

f0 =  = .

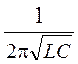Параметры L, C, RL,r контура указаны на стенде. Значения L, C и f0 запишите в табл. 1.

Таблица 1

№ п/п

Частота f, МГц

U0, В

R1 = ... Ом

R2 = ... Ом

1

2

…

11

C =        Ф

f0 =         кГц

L =        Гн

E0 =         В

3. Определите по осциллографу амплитуды вынужденных колебаний напряжения U0, снимаемого с конденсатора в делениях масштабной сетки на экране осциллографа, при фиксированных значениях частоты f генератора в выбранном диапазоне частот при R1. Полученные данные занесите в табл. 1.

4. Повторите опыт (пункт 3) при другом сопротивлении R2, включенном в контур.

5. Не изменяя настройки генератора, определите амплитуду колебаний э. д. с. генератора, соответствующую резонансной частоте, полученной экспериментально в п. 3, 4. Для этого установите на генераторе резонансную частоту, выход генератора подключите непосредственно к входу электронного осциллографа с помощью переключателя на стенде, и зафиксируйте амплитуду сигнала E0. Результат занесите в табл. 1 и табл. 2.

6. По данным табл. 1 постройте резонансные кривые при различных сопротивлениях контура R1 и R2.

7. На каждой резонансной кривой отметьте уровень, соответствующий 0,U0 РЕЗ.

Расчет добротности контура

8. По резонансным кривым, снятым экспериментально, определите частоты f1 и f2, соответствующие границам полосы пропускания контура и их разность Df = f2 - f1. Результаты измерений занесите в табл. 2.

Таблица 2

Сопротивление контура, Ом

R1

R2

U0 РЕЗ, В

0,7U0 РЕЗ, В

fРЕЗ, МГц

f1, МГц

f2, МГц

Df, МГц

Q1 =

E0, В

Q2 =

QСР = (Q1 + Q2)/2

QТЕОР = Q =

9. Вычислите значения добротности Q1 и Q2 по формулам (10) и (12) для различных значений сопротивлений контура. Результаты занесите в табл. 2.

10. Определите среднее арифметическое значение добротности при различных фиксированных значениях сопротивлений контура:

QСР = (Q1 + Q2)/2.

11. Оцените относительную погрешность определения добротности по косвенным измерениям:

dQ1 =  =  +  + ,

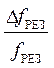dQ2 =  =  +,

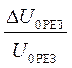где DfРЕЗ, Df1, Df2, DU0 РЕЗ, DE0 – ошибки в определении соответствующих значений fРЕЗ, f1, f2, U0 РЕЗ, E0.

Вычислите теоретическое значение добротности контура по формуле (9) и сравните его с результатами расчета по формулам (10) и (12). Объясните возможные причины расхождения результатов измерений и расчета.

Контрольные вопросы

1. Какие колебания называются вынужденными?

2. В чем заключается явление резонанса?

3. От чего зависит добротность контура?

4. Перечислите методы определения добротности контура.

5. Дайте определение полосы пропускания контура.

6. Чему равна частота вынуждающей э. д. с. в момент резонанса?

7. Каким образом снимается резонансная кривая в данной работе?

Список литературы

3.  Савельев И.В. Курс общей физики в 3-х тт. Т. 2. Электричество и магнетизм. Волны. Оптика. – М.: – Наука, 2005. – 496 с.

4.  Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

Работа 129

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

С ПОМОЩЬЮ ОСЦИЛЛОГРАФА

Цель работы. Изучение с помощью электронного осциллографа электромагнитных колебаний, возникающих в колебательном контуре, содержащем индуктивность, емкость и активное сопротивление; изучение условий возникновения затухающих колебаний в контуре; расчет основных физических величин, характеризующих эти колебания.

Введение

На рис. 1 изображена электрическая схема простейшего колебательного контура с сосредоточенными параметрами, содержащего последовательно соединённые конденсатор емкостью C, катушку индуктивностью L и активное сопротивление R.

Если в какой-либо момент времени одной из обкладок конденсатора сообщить электрический заряд или создать условия для возникновения в катушке электродвижущей силы (э. д. с.) индукции, а затем отключить источники возбуждения, в контуре начнутся свободные электромагнитные колебания.

Скачать файл