Методические указания к лабораторным работам "Изучение свободных колебаний связанной системы тел", "Изучение релаксационных электрических колебаний", "Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа", "Вынужденные колебания в последовательном электрическом контуре", страница 14

 + 2b + w₀²U = E₀w₀²cosWt,                       (3)

в котором b – коэффициент затухания; w₀ – собственная циклическая частота колебаний (при R = 0).

Решение данного дифференциального уравнения имеет вид:

U = U₀cos(Wt - y),                                      (4)

где:

U₀ = 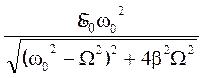,                               (5)

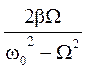tgy = .                                        (6)

Таким образом, амплитуда U₀ и начальная фаза y  вынужденных колебаний напряжения на конденсаторе зависят от частоты вынуждающей э. д. с.

Исследуя уравнение (5) на экстремум, можно показать, что разность потенциалов на конденсаторе достигнет максимума при частоте вынуждающей э. д. с., равной

W_РЕЗ = .                                       (7)

При этом максимальное значение амплитуды составляет

U_{0 РЕЗ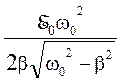} = .                                     (8)

Соотношение (8) имеет смысл только при w₀² > b².

Явление резкого возрастания амплитуды вынужденных колебаний напряжения при изменении частоты вынуждающей э. д. с. называется резонансом. Частота, при которой наступает это явление, называется резонансной частотой.

Кривая зависимости U₀ от W при заданном значении коэффициента затухания называется резонансной кривой. На рис. 2 представлено семейство резонансных кривых 1, 2, 3, соответствующих различным значениям коэффициента затухания b₁, b₂, b₃, при этом b₃ > b₂ > b₁.

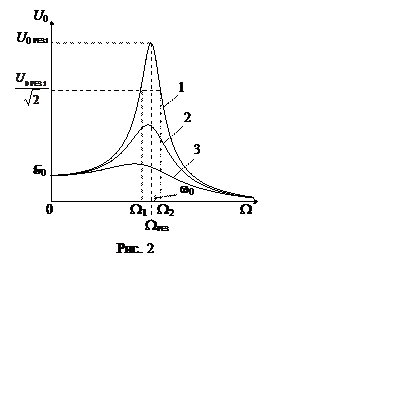Как следует из уравнения (5) и рис. 2, U₀ = E₀ при любом значении коэффициента затухания, если W = 0. Кроме того, резонансная частота при увеличении коэффициента затухания смещается в сторону меньших значений, а амплитуда напряжения, соответствующего резонансу, убывает с увеличением b.

Ток в контуре

I = C = CWU₀sin(Wt + y) = I₀cos(Wt + y₁),      где y₁ = y + .

Амплитуда тока в контуре зависит от соотношения частот W и w₀:

I₀ = 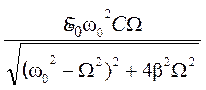                                  (9)

График зависимости I₀ от W представлен на рис. 3. Из графика видно, что амплитуда тока резко возрастает в момент резонанса при приближении циклической частоты W источника э. д. с. к частоте w₀. Это явление называется резонансом, а кривые – резонансными кривыми. Величина резонансной силы тока в контуре зависит от b: при b = 0 сила тока I_{0 РЕЗ} → ∞ (кривая 1); при увеличении b максимальное значение I_{0 РЕЗ} уменьшается (кривые 2 и 3), y₁ определяет разность фаз колебаний тока в контуре и внешней э. д. с.:

tgy₁ = tg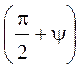 =  = 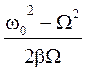.                    (10)

Следует отметить, что максимальное значение тока в рассматриваемом контуре достигается при одной и той же частоте W = w₀ при любых значениях b.

Остроту резонансных кривых характеризует добротность контура. При слабом затухании добротность контура Q можно определить как величину, равную произведению 2p на отношение запасенной в катушке индуктивности энергии W₀ к энергии тепловых потерь W_R в контуре за время, равное периоду T:

Q = 2p.

Если известны параметры контура, добротность может быть рассчитана по формуле:

Q =  = .                                   (11)

Методы определения добротности

Можно показать, что для контура, изображённого на рис. 1,

Q =  = ,                                  (12)

R_П = r + R + R_L,

где R_П – полное сопротивление цепи; r – внутреннее сопротивление источника тока; R – сопротивление резистора, включенного в контур; R_L – активное сопротивление катушки индуктивности.

1. Расчет теоретического значения добротности Q_ТЕОР

Добротность контура Q_ТЕОР можно рассчитать по формуле (12), зная параметры электрической цепи R_П, L и C.

2. Определение добротности по измерениям резонансного напряжения U_{0 РЕЗ} и амплитуды вынуждающей э. д. с. E₀

Соотношение (8) при малых коэффициентах затухания принимает вид

U_{0 РЕЗ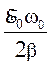} =  = E₀Q,    откуда

Q = 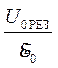.                                          (13)

3. Определение добротности по ширине резонансной кривой

Шириной резонансной кривой называется разность частот W₁ и W₂, при которых достигается эффективное значение резонансного напряжения на конденсаторе, равное (см. рис. 2) U₀ = .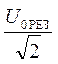

Разность этих частот DW = W₂ - W₁ называется полосой пропускания контура.

Можно показать, что:

Q » 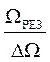.                                            (14)

Таким образом, зная DW и W_РЕЗ, можно вычислить добротность контура. Расчет добротности этим методом производится с помощью полученной экспериментально резонансной кривой, построенной в координатах U₀ , W: определяются значения W₁ и W₂, соответствующие напряжению U₀ = 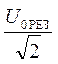 » 0,7U₀ слева и справа от максимума, после чего вычисляется их разность DW = W₂ - W₁.

В данной работе циклическим частотам W_РЕЗ, W₁ и W₂ соответствуют значения частоты генератора f = W/(2p) [Гц], поэтому

Q = 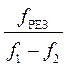.                                          (15)

Метод измерения и описание аппаратуры

Принципиальная электрическая схема лабораторной установки приведена на рис. 4.

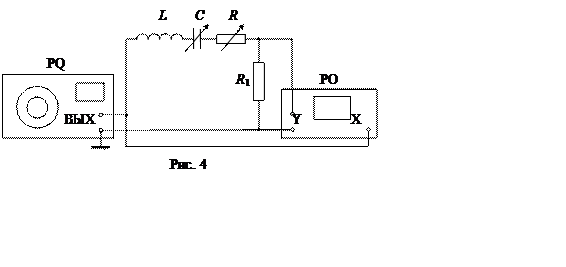Резонансные кривые снимают при различных сопротивлениях, включенных в контур. Сигнал с конденсатора подается на вход электронного осциллографа; при изменении частоты генератора на экране осциллографа измеряется амплитуда напряжения. Диапазон частот выбирается достаточно широким в обе стороны по отношению к резонансной частоте, которая соответствует наибольшей амплитуде измеряемого напряжения при заданном сопротивлении контура.

Определение добротности контура производится двумя способами: по ширине резонансной кривой и по отношению резонансного напряжения к амплитуде вынуждающей э. д. с. Полученные результаты позволяют вычислить омическое сопротивление контура и оценить значение внутреннего сопротивления генератора.

Принципиальная электрическая схема установки представлена на рис. 5: ФПЭ-11 – кассета; МС – магазин сопротивлений; МЕ – магазин емкостей; PQ – звуковой генератор; PO – осциллограф.

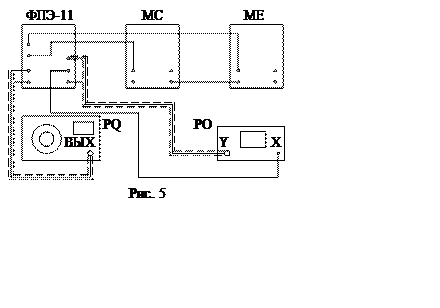Порядок выполнения работы

Задание 1. Снятие резонансных кривых