T0 = 2p/w0. (12)
При отсутствии трения величина А – постоянная во времени, колебания называются свободными незатухающими, а уравнения (9) и (10) – дифференциальными уравнениями свободных незатухающих колебаний.
Учет силы трения, всегда действующей в реальных механических системах, приводит к изменению уравнения (10). В нем появляется еще один член, и оно приобретает вид
+ 2b
+ w02y =
0, (13)
где b - коэффициент затухания. Решение уравнения (13) имеет вид
y = A0e-bt sin(w0t + a) или y = A0e-bt cos(w0t + a¢), (14)
где A0 – постоянная; A0 e-bt – убывающая амплитуда колебаний.
Таким образом любое механическое колебание происходит с затратами энергии на работу против сил трения. При этом амплитуда колебательного движения А с течением времени убывает, происходит затухание колебаний (рис. 2.)
Графически изменение амплитуды по времени изображается огибающей кривой затухающих колебаний (пунктирная линия на рис. 2).
Частота затухающих колебаний w отличается от частоты w0 незатухающих колебаний и равна
w = 
. (15)
Из этого следует, что период затухающих колебаний T = 2p/w больше периода незатухающих колебаний T0 = 2p/w0.
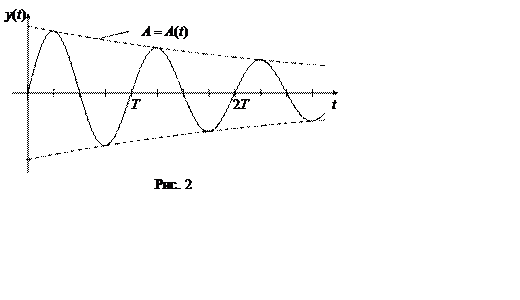
Методы измерений и описание аппаратуры
Система связанных между собой тел, изучаемая в данной лабораторной работе, состоит из пружины и груза, связанных невесомой и нерастяжимой нитью, перекинутой через блок. Блок укреплен на стойке со шкалой. На стойке со стороны груза укреплена дополнительная шкала на передвижном экране.
Коэффициент жесткости пружины k определяют, создавая статическое растяжение пружины под действием груза, прикрепленного к концу нити. При неподвижном грузе, действующая на него сила тяжести mg уравновешивается силой упругости пружины, растянутой на величину x, т. е. mg = kx.
Период затухающих колебаний Т определяют, измеряя время t нескольких полных колебаний n. Период рассчитывают по формуле T = t/n. Измерение времени проводят с помощью лабораторного секундомера.
Период незатухающих колебаний рассчитывают по формуле (12) и сравнивают с периодом затухающих колебаний.
Коэффициент затухания в данной работе определяют, используя закон убывания амплитуды А = A0e-bt = A0exp(-bt). Для этого измеряют число колебаний n1, за время которых амплитуда колебаний уменьшится в e раз. Напишем отношение амплитуд для моментов времени t и (t + n1Т) начала и конца опыта:
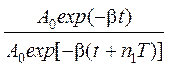= e.
Из этой формулы после простых преобразований следует
b=1/(n1Т). (16)
Порядок выполнения работы
I. Определение коэффициента жесткости пружины
1. К свободному концу нити подвесить подставку для грузов.
2. Определить по шкале положение дна подставки при отсутствии на ней грузов l0 (исходное состояние).
3. Последовательно нагружая подставку грузами, определять положение дна подставки l после очередного увеличения нагрузки.
4. Разгружать подставку, последовательно снимая с нее грузы, и определять по шкале положение дна подставки l' после очередного уменьшения нагрузки вплоть до нуля (l0').
5. Для каждого значения суммарной массы грузов на подставке (без массы подставки) записать в табл. 1 положение подставки при увеличении и уменьшении нагрузки. Записать его среднее значение lСР.
6. Для каждого значения массы грузов на подставке определить удлинение пружины.
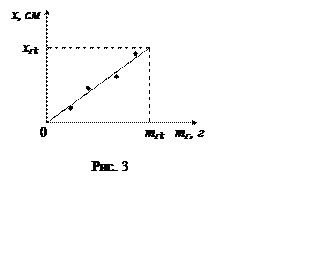7. Построить на миллиметровой
бумаге график зависимости удлинения пружины x от массы грузов на
подставке mГ, примерный вид которого дан на
рис. 3. По графику определить коэффициент жесткости пружины, используя формулу
k =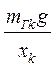 
,
где mГk и xk – стороны треугольника, изображенного на рис. 3, измеренные в граммах и сантиметрах. Коэффициент жесткости рассчитать в Н/м.
II. Определение периода колебаний системы
1. Положить на подставку несколько грузов. Записать массу грузов (с подставкой) и массу блока m0.
2. Привести систему в колебательное движение и измерить время t нескольких колебаний (n = 8 ё 10). Измерения проделать шесть раз, результаты занести в табл. 2.
3. Рассчитать значение периода Т при каждом измерении и найти его среднее значение.
4. Определить по формуле (12) период свободных незатухающих колебаний Т0 и сравнить его с измеренным средним периодом затухающих колебаний ТСР.
III. Определение коэффициента затухания
1. Отклонив груз от положения равновесия на некоторое расстояние А0, отпустить его и сосчитать число колебаний n1, за время которых амплитуда колебаний уменьшится в e раз.
При проведении этих измерений следует воспользоваться дополнительной шкалой на передвижном экране, укрепленном на стойке. Для этого следует установить ноль шкалы так, чтобы он находился против дна подставки с грузами.
Отклонив груз на расстояние А0 = 5 см, отпустить его и сосчитать число колебаний, для которых амплитуда будет оставаться большей или равной А = А0/e » 1,8 см. Это значение амплитуды отмечено на экране.
2. Повторить измерения несколько раз и найти среднее значение n1СР. Результаты записать в табл. 2.
3. Используя полученную ранее среднюю величину периода затухающих колебаний TСР, по формуле (17) вычислить коэффициент затухания
b СР = 1/(n1СР ТСР). (17)
IV. Обработка результатов измерений
1. Рассчитать случайную ошибку ΔT при определении периода колебаний по формуле
DT = a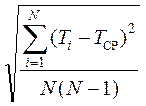
,
где коэффициент Стьюдента a при числе измерений N = 5 и доверительной вероятности 0,9 следует взять из соответствующих таблиц (см. [3]).
2. Рассчитать случайную ошибку Dn1 при определении n1СР – числа колебаний в опытах по измерению коэффициента затухания.
Расчет проделать по формуле
Dn1 = a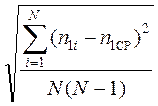
,
где b и N имеют те же значения, что и в пункте 1.
Таблица 1
|
№ п/п |
mГ, г |
l, см |
lў, см |
lСР, см |
x, см |
|
Исходное состояние |
0 |
||||
|
1 |
|||||
|
2 |
|||||
|
3 |
|||||
|
4 |
|||||
|
5 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.