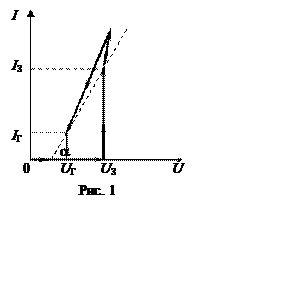Методические указания к лабораторным работам "Изучение свободных колебаний связанной системы тел", "Изучение релаксационных электрических колебаний", "Изучение затухающих электромагнитных колебаний в колебательном контуре с помощью осциллографа", "Вынужденные колебания в последовательном электрическом контуре", страница 4

Для упрощения расчетов можно взять идеализированную характеристику неоновой лампы, которая представляет собой отрезок прямой линии, проходящей через точки I_Г, U_Г и I_З, U_З и пересекающей ось напряжений Uпод углом  a. По идеализированной характеристике можно численно определить внутреннее сопротивление лампы:

R_i = ctga = (U_З - U_Г)/(I_З - I_Г).

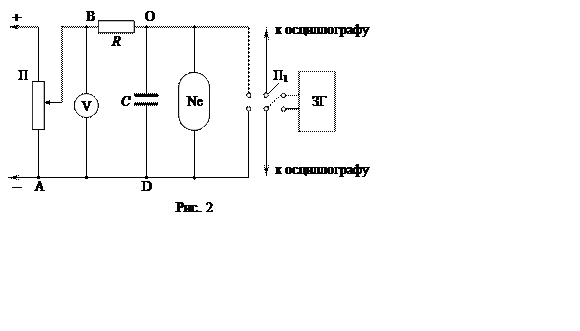
Рассмотренные свойства неоновой лампы позволяют объяснить механизм возникновения релаксационных колебаний в схеме, приведенной на рис. 2.

Пусть в начальный момент времени (t =0) напряжение на конденсаторе С равно нулю и неоновая лампа (Ne) не горит (ее внутреннее сопротивлениеR_i= ¥).

После подключения источника тока конденсатор С заряжается и напряжение на нем возрастает по кривой ОА (рис. 3а), стремясь стать равным напряжению, снимаемому с потенциометра U_П. Но раньше, чем оно достигнет этого значения, лампа зажжется. Это произойдет при напряжении U = U_З. При этом внутреннее сопротивление R_i неоновой лампы скачком становится конечным, численно равным ctga (см. рис. 1). После этого начинается разряд конденсатора, причем напряжение на обкладках конденсатора падает по экспоненте АВ, стремясь асимптотически сравняться с некоторым предельным значением U_ПР. Однако при напряжении U_Г, несколько большим U_ПР, лампа гаснет, то есть внутреннее сопротивление скачком принимает значение R_i = ¥, и конденсатор снова начинает заряжаться, причем напряжение на нем растет по кривой ВС. Когда напряжение на обкладках конденсатора станет равным U_З, лампа снова зажжётся. Дальше процесс повторяется периодически.

Как видно из рис. 3а, зависимость напряжения от времени представляет собой непрерывную кривую, в то время как соответствующая кривая тока носит разрывный характер. Колебания тока, представленные на рис. 3б, и называются разрывными или релаксационными.

Следует заметить, что релаксационные колебания в схеме, представленной на рис. 2, могут возникнуть, если параметры неоновой лампы U_З и U_Г лежат внутри интервала асимптотических значений U_ПР и U_П, то есть при выполнении следующего условия:

U_ПР < U_Г < U_З < U_П.

Составим дифференциальное уравнение, которое описывает процесс релаксационных колебаний в приведенной на рис. 2 схеме. Для этого применим второе правило Кирхгофа к замкнутому контуру ABOD:

IR + U_C = U_П.

Подставляя в это уравнение известные соотношения

I = dq/dt  и  U_С = q/C,

получим следующее дифференциальное уравнение:

RC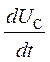 + U_C = U_П.                                       (1)

Решение уравнения (1) при начальных условиях t = 0, U = 0 имеет вид

U_C = U_П(1 - ).                                        (2)

Произведение RC называется постоянной времени цепи.

Период релаксационных колебаний Т складывается из времени зарядки конденсатора t_З и времени его разрядки t_Р:

Т = t_З + t_Р.

Время зарядки конденсатора в процессе колебаний может быть определено как:

t₃ = t₂ – t₁,

где t₂ – время зарядки конденсатора до напряжения U_З, t₁ – время зарядки конденсатора до напряжения U_Г (см. рис. 3а).

Значения t₂ и t₁ определяются из формулы (2):

U_З = U_П(1 - );                  U_Г = U_П(1 - ).

Отсюда

t₂ = -RC×ln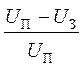;    t₁ = -RC×ln.

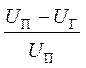Следовательно,

t₃ = t₂ - t₁ = RC×ln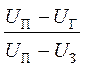.                               (3)

Время разрядки определим по аналогичной формуле (считая, что U_ПР = 0)

t_Р = R_iC×ln.                                          (4)

Если выбирать сопротивление R достаточно большим (R >> R_i), то t_Р будет много меньше t_З, и период релаксационных колебаний можно считать равным

T » t₃ = RC×ln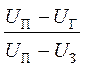.                                   (5)

Из (5) следует, что период колебаний пропорционален постоянной времени RC.

Таким образом, измеряя U_П, U_З и U_Г и зная электрические параметры схемы, можно определить период релаксационных колебаний.

Релаксационные электрические колебания нашли многочисленные практические применения в радиотехнике и измерительной технике. Они используются для измерения неизвестных сопротивлений и емкостей, для измерения частоты в широких пределах, используются для создания генераторов пилообразных колебаний, применяемых в электронных осциллографах и т.д.

Порядок выполнения работы

I. Снятие вольтамперной характеристики неоновой лампы

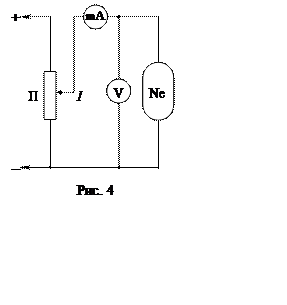
1. Соберите схему, изображенную на рис. 4. Изменяя потенциометром П напряжение на лампе (Ne), измерьте силу тока в цепи. Результаты занесите в табл. 1.

Таблица 1

№	1	2	3	4	5	6	7	8	9	10
U, В
I, мА

2. По данным табл. 1 постройте вольтамперную характеристику лампы, т.е. зависимость I= f(U).

3. Пользуясь вольтамперной характеристикой, определите напряжение зажигания U_З и ток зажигания I_З, напряжение гашения U_Г и ток гашения I_Г лампы, а также вычислите внутреннее сопротивление лампы

R_i = (U_З – U_Г)/(I_З – I_Г).

Результаты занесите в табл. 2.

Таблица 2

UЗ,  В	IЗ,  мА	UГ,  В	IГ,  мА	Ri, Oм

II. Наблюдение формы релаксационных колебаний и исследованиезависимости периода колебаний от параметров контура R и С

1. Соберите схему, изображенную на рис. 2.

2. С помощью переключателя П₁ подключите к Y-входу осциллографа неоновую лампу.

3. Получите на экране осциллографа устойчивую неподвижную картину релаксационных колебаний при заданных R и С, подбирая напряжение на неоновой лампе потенциометром П и изменяя частоту развертки осциллографа. Зарисуйте полученную кривую.

4. Повторите опыт по п. 3 для различных комбинаций R и С.

5. Рассчитайте время зарядки и время разрядки конденсатора по формулам (3) и (4) при фиксированных значениях R, C и U_П. Величины напряжений зажигания и гашения возьмите из табл. 2. Полученные данные занесите в табл. 3.

Таблица 3