

































ков для режима холостого хода. Характер зависимости Rвх.кз и Хвх.кз от длины линии с потерями определяется теми же причинами, что и в случае режима холостого хода.
На рис. 9.19 приведены схемы применения короткозамкнутых отрезков линий в двухпроводной и коаксиальной линиях и в полуволновом симметричном вибраторе.
В двухпроводных и коаксиальных линиях передачи, а также в некоторых типах антенн в качестве опорных конструктивных элементов применяются так называемые «металлические изоляторы». Эти «изоляторы» представляют собой четвертьволновые отрезки короткозамкнутых линий. Входное сопротивление такого отрезка, как видно на рис. 9.18, б, может достигать очень большого значения. При подключении отрезка параллельно к линии в некотором ее сечении как опорного элемента (см. рис. 9.19, а) ток на его входе имеет незначительную величину, и мощность из основной линии в отрезок практически не ответвляется. Такой опорный элемент выполняет функции металлического изолятора в узкой полосе частот, так как при изменении частоты (длины волны) его входное сопротивление быстро уменьшается (рис. 9.18, б).
Линия с реактивной нагрузкой. Если к концу идеальной линии подключена реактивная нагрузка, то поглощения энергии падающей волны в ней не происходит и отраженная волна по амплитуде равна падающей. В этом случае в линии возникает стоячая волна. Однако для реактивного сопротивления нагрузки Хн ≠ 0 ни напряжение, ни ток в конце линии в нуль не обращаются. Следовательно, сдвиг фаз отраженных волн напряжения и тока лежит между 0 и 180° и определяется значением реактивного сопротивления нагрузки.
Проанализируем распределение входного сопротивления, напряжения и тока в идеальной линии с реактивной нагрузкой Хн < 0 и Хн > 0 (рис. 9.20).
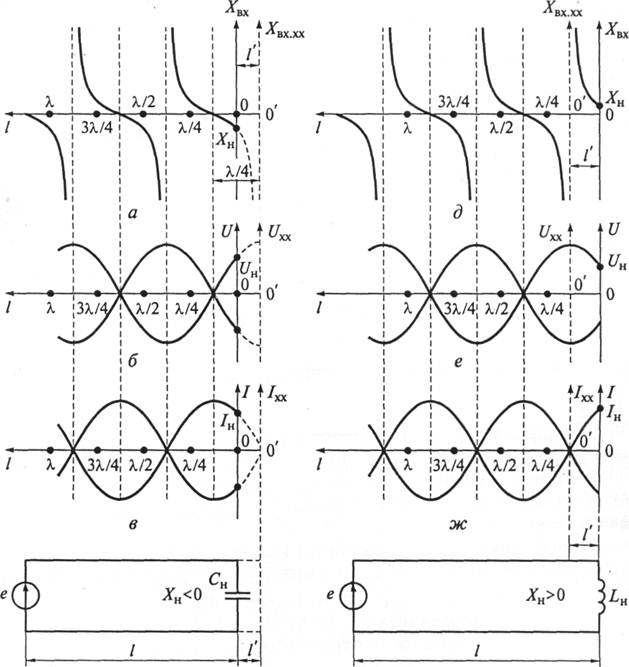
Пусть линия нагружена на конечное емкостное сопротивление Хн < 0. Ранее установлено, что входное сопротивление идеальной разомкнутой линии на участке от ее конца х = 0 до сечения х = λ/4 изменяется от - ∞ до нуля (см. рис. 9.20, а).
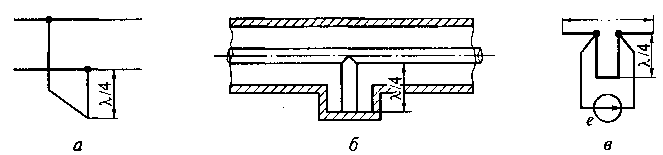
Рис. 9.19. Схемы применения короткозамкнутых отрезков линий в двухпроводной (а) и коаксиальной (б) линиях и в полуволновом симметричном вибраторе (в)
г з
Рис. 9.20. Распределение входного сопротивления (а, д), напряжения (б, е) и тока (в, ж) в идеальной линии с реактивной нагрузкой Хн < 0 (г) и Хн > 0 (з)
Значит, на этом участке найдется некоторое сечение х = l', для которого выполняется условие Хвх = Хн. Тогда согласно (9.15) Хн = -Wctg(bl') или
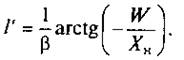 (9.17)
(9.17)
Если отрезок длиной l' в конце линии заменить емкостным сопротивлением Хн, то распределение эквивалентного сопротивления в линии не изменится (см. рис. 9.20, а). Не изменятся также распределения напряжения и тока, но значения амплитуд напряжения Uни тока Iн на нагрузке, как это видно на рис. 9.20, б, в, будут отличаться от случая холостого хода.
При подключении к концу линии индуктивной нагрузки Хн > 0 из (9.17) следует, что l' < 0. Это означает, что распределения эквивалентного сопротивления, напряжения и тока в линии останутся неизменными при переходе от разомкнутой линии к линии, нагруженной на индуктивное сопротивление Хн, если последнее будет подключено к концу линии, удлиненной на отрезок длиной l' (см. рис. 9.20, д, е, ж). Однако напряжение и ток на нагрузке, как и в предыдущем случае, претерпят изменения.
На рис. 9.20 видно, что хотя в целом картина распределения эквивалентного сопротивления, напряжения и тока в идеальной линии с реактивной нагрузкой такая же, как и в разомкнутой линии, но узлы и пучности напряжения и тока, а также нулевые и бесконечно большие значения эквивалентного сопротивления находятся в сечениях, отстоящих от конца линии на расстоянии, не кратном λ/4.
9.7. Параметры, характеризующие режим работы длинной линии
Для характеристики режимов работы длинной линии в радиотехнике используют коэффициенты отражения, бегущей и стоячей волны, полезного действия линии. Рассмотрим определения этих параметров, их связь с режимами работы линии и взаимосвязь между собой.
Коэффициентом отражения по напряжению называется отношение значений комплексных амплитуд напряжений отраженной и падающей волн. Коэффициент отражения Г = Гехр(jξ) является комплексной величиной с модулем Г и фазой (аргументом) ξ.
При анализе процессов отражения бегущих волн от конца разомкнутой или короткозамкнутой линии установлено, что одна из отраженных волн обязательно получает сдвиг фаз на 180°, т.е. изменяет свой знак на противоположный. Поэтому для коэффициента отражения можем записать Г = Uотр/ Uпад =Iотр/ Iпад . Величину Гi = Iотр/ Iпад называют коэффициентом отражения по току. Из двух последних равенств следует, что Г = - Гi, т.е. фазы коэффициентов отражения по напряжению и току противоположны.
В идеальной линии амплитуды падающей и отраженной волн остаются постоянными, поэтому в такой линии модуль коэффициента отражения будет одинаков в любом ее сечении. Аргумент коэффициента отражения, являясь разностью фаз напряжений отраженной и падающей волн, линейно зависит от координаты сечения линии.
В линии с потерями амплитуда падающей волны напряжения убывает от генератора к нагрузке, а амплитуда отраженной волны в том же направлении возрастает. Вследствие этого модуль коэффициента отражения изменяется вдоль линии: он монотонно возрастает от генератора к нагрузке.
В соответствии с определением модуль коэффициента отражения в линии, подключенной к пассивной нагрузке, является положительной величиной, не превышающей единицу.
В теории длинных линий часто пользуются значениями коэффициента отражения от нагрузки Гн = Uн.отр/ Uн.пад = -Iн.отр/ Iн.пад . Комплексные амплитуды тока и напряжения на нагрузке можно выразить через комплексные амплитуды падающих и отраженных волн: Uн = Uн.отр + Uн.пад = - Iн Zн, Iн = (Uн.пад - Uн.отр)/W. Используя эти соотношения, можно выразить коэффициент отражения от нагрузки через волновое сопротивление линии И7 и сопротивление нагрузки Zн: Гн = (Zн - W)/(Zн+ W). Полученная формула справедлива для произвольного комплексного сопротивления нагрузки.
В режиме бегущей волны в идеальной линии Zн = W и Гн = 0 , т.е. коэффициент отражения от нагрузки равен нулю, и отраженная волна отсутствует.
В режиме холостого хода Zн → ∞ и поэтому Гн = (Zн - W)/(Zн+ W) = (1 – (W/ Zн))/ (1 + (W/ Zн)) = 1, или Гн = Гн ехр(jξн) = 1, где Гн и ξн — модуль и фаза коэффициента отражения от нагрузки. Следовательно, для падающей волны напряжения Гн = 1 и ξн = 0, а для падающей волны тока Гiн = 1 и ξiн = π. Таким образом, волна напряжения отражается с той же амплитудой и фазой, а волна тока при отражении амплитуду сохраняет, а фазу изменяет на π .
В режиме короткого замыкания Zн = 0 и при этом Гн = ехр(jπ) = -1. В этом случае волны напряжения при отражении от конца линии амплитуду сохраняют, а фазу изменяют на π. Волна тока при отражении сохраняет как амплитуду, так и фазу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.