Основной тип волны в СЩЛ характеризуется большим значением продольной составляющей магнитного поля Hz, направленной вдоль щели. Такая волна называется Н-волной. Поле этой волны концентрируется вблизи щели. Особенностью основного типа волны в СЩЛ является то, что компоненты ее магнитного поля Нх и Hzсдвинуты по фазе на 90°, т.е. магнитное поле волны эллиптически поляризовано. Это свойство широко используется для создания на базе СЩЛ ферритовых устройств (вентилей, циркуляторов) для управления распространением сигналов в ИМС СВЧ.
В СЩЛ по сравнению с МПЛ более сильно выражена дисперсия основного типа волны. При одинаковых отношениях w/hволновое сопротивление Wимеет большие значения, конструктивно удобнее вести монтаж навесных компонентов. Потери в СЩЛ значительно ниже, чем в МПЛ, так как токонесущие проводники имеют большую поверхность. Более высокие значения волнового сопротивления СЩЛ облегчают согласование с ней различных устройств и компонентов СВЧ.
На практике в ИМС СВЧ часто применяют комбинации различных типов полосковых линий, используя особенности и положительные свойства каждой из них.
10.4. Волноводы
Рассмотренные линии передачи (кроме некоторых типов полосковых линий) объединяет одно свойство: в рабочем диапазоне частот в них распространяются только поперечные электромагнитные волны, т.е. Т-волны.
Линии передачи с Т-волнами обладают рядом положительных свойств. Электромагнитные колебания могут распространяться в них, начиная с нулевой частоты, т.е. по ним может протекать постоянный ток. Это возможно вследствие наличия у рассмотренных типов линий двух или более не связанных между собой проводников. Фазовая скорость волн в таких линиях, если диэлектриком является воздух, не зависит от частоты, т.е. в линиях передачи с Т-волнами дисперсия отсутствует. В подобных линиях широкополосные сигналы распространяются практически без искажения своей формы на достаточно большие расстояния.
При повышении частоты для сохранения режима распространения Т-волн в линии передачи необходимо уменьшать размеры ее поперечного сечения. Такое уменьшение поперечных размеров линии сопровождается увеличением потерь, снижением электрической прочности и, соответственно, уменьшением предельного значения мощности, передаваемой по линии. Вследствие этого в сантиметровом и миллиметровом диапазонах волн при передаче больших мощностей применение линий передачи с Т-волнами становится затруднительным. В этих диапазонах более эффективным является применение других типов линий передачи — волноводов, представляющих собой полые металлические трубы с прямоугольной, круглой, эллиптической и другими формами поперечного сечения (рис. 10.6).
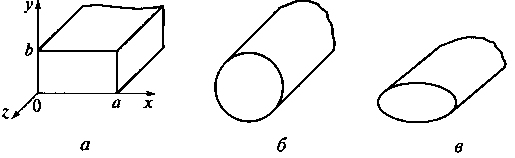
Рис. 10.6. Прямоугольный (а), круглый (б) и эллиптический (в) полые волноводы
В полых металлических волноводах Т-волны распространяться не могут, так как в их конструкции нет двух или более изолированных проводников. В волноводах распространяются волны, которые кроме поперечных составляющих векторов Е и Н, лежащих в плоскости поперечного сечения волновода, содержат и продольные их составляющие, направленные вдоль оси волновода (по направлению распространения волны). Названия этих волн зависят от их структуры.
Е-волной называется электромагнитная волна, у которой продольную компоненту имеет только вектор напряженности электрического поля. Н-волной называется электромагнитная волна, у которой продольную компоненту имеет только вектор напряженности магнитного поля. Гибридной (смешанной) НЕ-волной называется электромагнитная волна, у которой продольные компоненты имеют одновременно оба вектора электромагнитного поля Е и Н.
Отмеченные типы волн возникают в волноводах при определенных условиях и обладают свойствами, существенно отличающимися от свойств Т-волн. Рассмотрим эти свойства на примере прямоугольного металлического волновода.
Прямоугольный волновод. Рассмотрим бесконечный прямоугольный волновод с поперечными размерами а и bи связанную с ним прямоугольную систему координат, показанные на рис. 10.6, а. В таком прямоугольном волноводе, выполненном из идеально проводящего металла, могут существовать только Е- или Н- волны,
При возбуждении Е- или Н-волны в прямоугольном волноводе поле в направлении разных координатных осей будет иметь разный характер. Так как по оси 0z волновод не ограничен, то по аналогии с волновыми процессами в длинной линии поле в этом направлении будет иметь характер бегущей волны. По осям 0x и 0yволновод ограничен идеально проводящими стенками, на которых для электромагнитного поля выполняются условия, аналогичные условию короткого замыкания в длинной линии. Поэтому в этих направлениях поле будет иметь характер стоячей волны. Для описания электромагнитных процессов в полых волноводах нельзя пользоваться понятием напряжения, так как оно применимо только к потенциальным полям (в частности к полям T-волн), а переменное электромагнитное поле в полых волноводах таковым не является. Вместо понятий «напряжение» и «ток» при анализе полей в волноводах используют соответствующие им первичные характеристики: напряженности электрического и магнитного полей. В соответствии с этим в прямоугольном волноводе вдоль осей 0x и 0yнапряженность продольной компоненты электрического поля будет изменяться по закону синуса (принимая нулевое значение на боковых стенках волновода), а напряженность продольной компоненты магнитного поля — по закону косинуса (достигая максимального значения на боковых стенках волновода).
Для комплексной амплитуды продольной компоненты вектора напряженности электрического поля в E-волне справедливо выражение
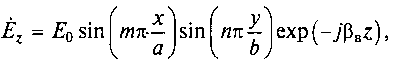(10.1)
где E0— амплитудное значение продольной компоненты вектора Eв волноводе; а и b — размеры волновода по осям 0x и 0y(см. рис. 10.6, a); βв — фазовый коэффициент бегущей волны в волноводе.
Комплексные амплитуды поперечных компонентов векторов Eи H в E-волне выражаются через продольную компоненту Ez, и их поведение в пространстве внутри волновода также подчиняется указанным выше закономерностям.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.