Основные типы длинных линий. Колебательные системы с распределенными параметрами (10-11 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 7

Для комплексной амплитуды продольной компоненты вектора напряженности магнитного поля в H-волне имеем

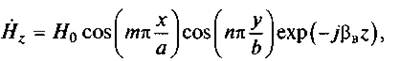(10.2)

где H₀ — амплитудное значение продольной компоненты вектора H в волноводе. Поперечные компоненты поля в H-волне выра­жаются через продольную компоненту H_z и также подчиняются описанным выше закономерностям.

Целые положительные числа т и n, не равные нулю в выраже­нии (10.1) и не обращающиеся одновременно в нуль в выраже­нии (10.2), характеризуют структуру поля в поперечном сечении волновода и называются индексами типа колебаний. Они определя­ют число полуволн (или иначе вариаций поля) в стоячей волне, укладывающихся соответственно вдоль размеров а и bпоперечно­го сечения волновода. Поле определенного типа Е- или H-волны с конкретным набором индексов т и п называется модой и обо­значается соответственно Е_тп или Н_тп. Так как значения чисел т и п сверху не ограничены, то и количество мод каждого из типов волн в прямоугольном волноводе тоже не ограничено.

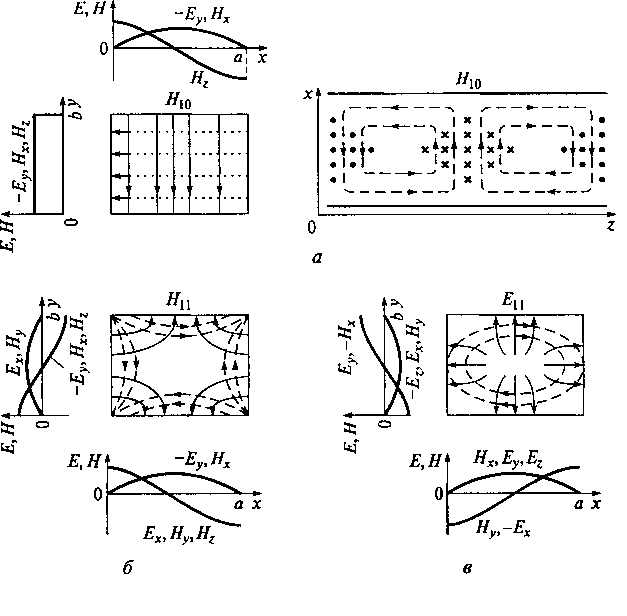
Структура силовых линий поля в плоскости поперечного сече­ния волновода для некоторых мод с малыми значениями индек­сов т и п, а также в плоскости продольного сечения волновода для моды H₁₀ показаны на рис. 10.7.

Силовые линии магнитного поля в волноводе всегда образуют замкнутые кривые, а силовые линии электрического поля либо замк­нуты, либо начинаются и заканчиваются на металлических стенках волновода, являясь перпендикулярными к ним на их поверхности.

На рис. 10.7 для каждой моды показаны графики зависимости амплитуд поперечных составляющих поля от координат х и у. Вид­но, что эти зависимости соответствуют стоячим волнам в направ­лениях осей абсцисс и ординат в волноводе. Частичное исключе­ние из этого правила составляют моды H_m0, У которых попереч­ные составляющие поля вдоль оси ординат не изменяются, о чем свидетельствует равенство нулю индекса п.

Структура силовых линий поля в поперечном сечении волно­вода для высших мод Е_тп и Н_тп получается повторением соответ­ственно структур мод Е₁₁и H₁₁ т раз по оси абсцисс и п раз по оси ординат. Иллюстрацией этого правила является рис. 10.8, на котором показана структура силовых линий поля моды колебаний H₂₂ в плоскости поперечного сечения прямоугольного волновода.

-----E------Н

Рис. 10.7. Структура силовых линий поля низших мод колебаний в плос­кости поперечного и продольного сечения прямоугольного волновода для волн типа Н₁₀ (а), Н₁₁ (б) и Е₁₁ (в)

Каждой моде колебаний Е_тп и Н_тп в волноводе соответствует своя критическая длина волны, определяемая выражением

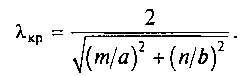(10.3)

Физический смысл этого параметра состоит в том, что мода колебаний с индексами т и п может существовать в волноводе лишь при условии λ < λ_кр, где λ_кр — длина волны колебаний генера­тора в безграничной среде с относительными проницаемостями ε и μ, соответствующими среде, заполняющей волновод. В против­ном случае данная мода колебаний в волноводе с идеально про­водящими стенками возбуждаться не будет. Заполнение внутрен­него пространства волновода диэлектриком с параметрами ε и μ уменьшает длину волны генератора в √εμ раз, что позволяет использовать волновод с заданной мо­дой колебаний при тех же размерах на более низких частотах.

Электромагнитные процессы, про­исходящие в идеальном волноводе при изменении частоты (длины) волны, можно рассмотреть с по­мощью соотношений (10.1) и (10.2), проанализировав выражение β_в = для фазового коэффициента волны, называемого также постоянной распространения.

При λ < λ_кр постоянная распрост­ранения β_в является действительной положительной величиной. В этом случае из (10.1) и (10.2) следу­ет, что поле внутри волновода вдоль оси 0_z имеет характер бегу­щей волны, а в поперечном сечении — структуру стоячей волны. Энергия электромагнитного поля переносится волной в положи­тельном направлении оси 0_z. Колебания электрического и маг­нитного полей в волне синфазны.

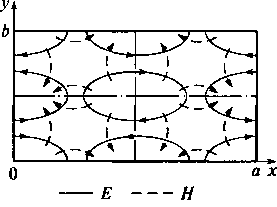
Рис. 10.8. Структура силовых линий поля моды колебаний Н₂₂ в плоскости поперечного сечения прямоугольного вол­новода

Если λ = λ_кр,  то β_в = 0. При этом поле теряет характер бегущей волны и приобретает структуру стоячей волны. Колебания элект­рического и магнитного полей сдвинуты по фазе на 90°. Энергия поля по волноводу не передается, она как бы законсервирована в форме стоячей волны в его внутреннем объеме. Между электри­ческим и магнитным полями в процессе колебаний происходит постоянный обмен энергией (как в колебательном контуре). В те­чение четверти периода колебаний осуществляется полное пре­вращение энергии поля в волноводе из электрической формы в магнитную (и наоборот).

Если реализуется условие λ > λ_кр, то постоянная распростране­ния β_в становится мнимой величиной. При этом комплексные ам­плитуды полей теряют характер бегущей волны и затухают вдоль оси волновода. В плоскости поперечного сечения волновода поле, как и в двух предыдущих случаях, имеет структуру стоячей волны со всеми характерными для нее свойствами.

Электромагнитные процессы в волноводе при λ = λ_кр и λ > λ_кр во многом подобны. Отличие состоит лишь в том, что в первом случае амплитуда стоячей волны вдоль оси волновода не меняется, а во втором — убывает. Волновод, работающий при условии λ > λ_кр, называется запредельным и используется в качестве аттенюатора (ослабителя) электромагнитных колебаний.

В запредельном режиме работы волновода ослабление поля в нем связано не с поглощением электромагнитной энергии, кото­рое в идеальном волноводе отсутствует, а с отражением большейчасти энергии от входа волновода обратно к источнику колеба­ний. В критическом режиме работы волновода при λ = λ_кр после окончания переходных процессов и установления стационарных колебаний в стоячей волне энергия полностью отражается от вхо­да волновода к источнику колебаний.