В реальных волноводах происходит поглощение энергии электромагнитного поля из-за конечной проводимости металлических стенок и остаточной проводимости заполняющей волновод диэлектрической среды. В этом случае электромагнитное поле в запредельном режиме может существовать в виде бегущих волн, однако амплитуда этих волн резко затухает вдоль оси волновода. Передача информации на значительные расстояния с помощью таких волн в волноводе невозможна.
Критические длины волн для всех возможных мод колебаний в волноводе образуют на оси длин волн бесконечную дискретную последовательность значений. При этом расстояние между соседними значениями критических длин волн уменьшается с ростом значений индексов т и п. Чем меньше длина волны колебаний генератора λ, тем для большего числа волноводных мод выполняется условие λ < λкр, и, следовательно, тем большее число мод может одновременно существовать в волноводе.
Моды колебаний в волноводе, имеющие одинаковые критические длины волн, называются вырожденными. Из соотношения (10.3) видно, что моды Е- и Н-волн с одинаковыми индексами т и п всегда вырождены.
Для снижения количества вырожденных мод на практике чаще всего применяются прямоугольные волноводы с соотношением поперечных размеров b= 0,5а. На рис. 10.9 показаны критические длины волн и область существования мод с малыми индексами в прямоугольном волноводе при b= 0,5а.
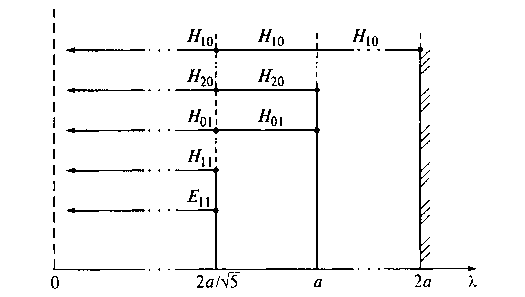
Рис. 10.9. Критические длины волн и область существования мод с малыми индексами в прямоугольном волноводе при b = 0,5а.
В частности, на рис. 10.9 указаны первые значения из ряда критических длин волн и соответствующие им моды, для каждой из которых стрелками указана область ее существования. Наибольшую критическую длину волны λкр = 2а имеет мода Н10, которая называется низшим или основным типом волны. Все другие моды, имеющие меньшие критические длины волн, называются высшими. Основной тип волны прямоугольного волновода обладает особым свойством: в диапазоне длин волн генератора а < λ < 2а в волноводе может устойчиво распространяться только этот тип волны. При более коротких длинах волн генератора в волноводе кроме основного типа волны всегда существуют и высшие моды колебаний, и их тем больше, чем короче волна генератора. Область длин волн при λ >2а называется областью отсечки, так как при этом условии волны в идеальном волноводе распространяться не могут.
Основными параметрами волноводных мод помимо критической длины волны являются также следующие:
а) фазовая Vви групповая Vгр скорости волны в волноводе:
|
(10.4)
|
(10.5)
в) характеристическое сопротивление для Е- и Н-волн:
![]() (10.6)
(10.6)
где Vфи λ — фазовая скорость и длина волны в неограниченном пространстве, заполненном той же средой (с электромагнитными параметрами ε и μ), что и внутреннее пространство волновода.
Из выражения (10.4) следует, что фазовая скорость моды зависит от критической длины волны λкр и от рабочей длины волны λ. Первая зависимость означает наличие в волноводе межмодовой дисперсии, а вторая — внутримодовой дисперсии. На распространение широкополосных сигналов в волноводе наиболее сильное влияние оказывает межмодовая дисперсия. Если при передаче сигналов по волноводу возбуждается сразу несколько мод, каждая из которых распространяется со своей фазовой скоростью, то это может привести к существенному искажению формы сигнала и потере информации. Для устранения этого явления выбирают такой режим работы, при котором в волноводе может распространяться только основной тип волны Н10.
Фазовая скорость распространяющейся моды в прямоугольном волноводе выше скорости света в безграничной среде, заполняющей волновод, т.е. Vв/Vф = 1/ √1-(λ/λкр)2 > 1. Этот факт не противоречит постулатам теории относительности, так как фазовая скорость не связана с движением материальных объектов или переносом энергии. Она является скоростью движения воображаемого объекта — плоскости фазового фронта волны.
Волны, для которых выполняется условие Vв/Vф > 1, называются быстрыми.
Скорость передачи информации по волноводам с помощью радиосигналов связана с понятием групповой скорости волн. Для уяснения этого понятия рассмотрим распространяющийся по волноводу узкополосный радиосигнал с равномерным спектром шириной 2Δω и центральной частотой ω0 (2 Δω << ω0). Такой сигнал можно представить как сумму гармонических волн с одинаковыми амплитудами и начальными фазами и близкими частотами, непрерывно заполняющими интервал 2Δω. Зависимость напряженности электрического поля в таком сигнале от продольной координаты zволновода в фиксированный момент времени имеет форму, показанную на рис. 10.10, на котором изображена пространственная форма группового сигнала в фиксированный момент времени.
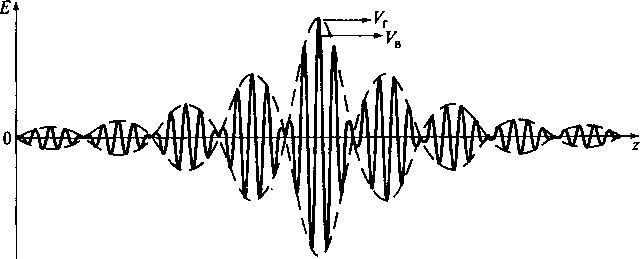
Рис. 10.10. Пространственная форма группового сигнала в фиксированный момент времени
Этот сигнал представляет собой гармоническое колебание с частотой ω0, промодулированное по амплитуде функцией, подобной функции (sinx)/x и являющейся огибающей группового сигнала. Для такого группового сигнала фазовая скорость есть скорость перемещения фазового фронта гармонической волны с частотой ω0, а скорость перемещения максимума огибающей называется групповой скоростью. Так как максимум огибающей соответствует пространственному положению максимума энергии, переносимой групповым сигналом, то групповая скорость характеризует скорость переноса энергии, т.е. скорость передачи информации. Поэтому групповая скорость волн не может превышать скорость света.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.