Для повышения добротности разомкнутых полосковых резонаторов (особенно полуволновых) их изгибают в виде подковы (см. рис. 11.4, в). Сближение противофазных по электрическому полю торцов резонатора существенно снижает потери на излучение. Однако при уменьшении зазора sмежду торцами растут потери в проводнике резонатора (из-за эффекта близости). Поэтому суммарные потери резонатора на излучение и в проводниках при определенной величине зазора sимеют минимум, а добротность — максимум. Подковообразные разомкнутые резонаторы при оптимальной ширине зазора sимеют добротность на 55 % выше, чем прямолинейные, и являются более компактными.
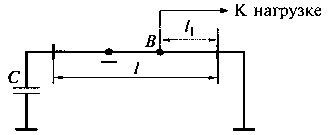
Рис. 11.5. Схема неполного включения нагрузки в короткозамкнутый полосковый резонатор
Расчет параметров эквивалентного колебательного контура полосковых прямоугольных резонаторов осуществляется так же, и для двухпроводных резонансных линий с помощью соотношений, приведенных в подразд. 11.2.
Полная добротность нагруженного резонатора (добротность эквивалентного контура) определяется из соотношения 1/Qэкв = 1/Q0 + 1/Qвн, где Q0— собственная добротность ненагруженного резонатора; Qвн — внешняя добротность резонатора, обусловленная потерями мощности в нагрузке.
Для заданной конструкции полоскового резонатора величину полной добротности Qэкв можно регулировать, изменяя внешнюю добротность Qвн, обусловленную отбором мощности из резона в нагрузку. Это осуществляется с помощью неполного включения нагрузки в резонатор. Для примера на рис. 11.5 приведена схема неполного включения нагрузки в короткозамкнутый полосковый резонатор на несимметричной полосковой линии, один конец которого нагружен на укорачивающий конденсатор С.
 б
б
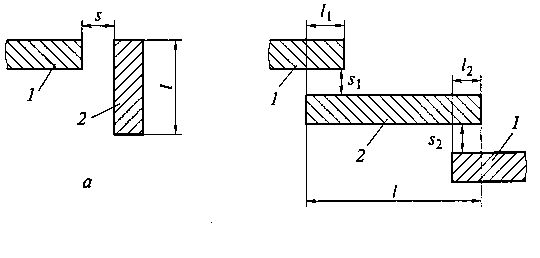
Рис. 11.6. Варианты включения полоскового резонатора в линию схеме двух- (а) и четырехполюсника (б): 1— полосковая линия; 2— резонатор
Благодаря этому конденсатору резонатор имеет длину l < λ/4. Кроме того, конденсатор С может быть использован доя перестройки резонатора.
При неполном включении нагрузка подключается к резонатору в точке В на расстоянии l1от короткозамкнутого конца. Изменяя положение точки В, можно регулировать степень включения нагрузки в резонатор, а следовательно, и величину добротности Qвн. При l1 = l из резонатора в нагрузку отбирается максимальная мощность, а добротность Qвн имеет минимальное значение Qвн = ω0СэквRн, где Rн — активное сопротивление нагрузки; Сэкв — емкость эквивалентного контура резонатора. Полная добротность резонатора Qэкв при этом также минимальна. При уменьшении длины l1 добротность Qвн растет, а вместе с ней растет и полная добротность резонатора Qэкв, приближаясь к собственной добротности Q0.
В интегральных схемах СВЧ микрополосковые резонаторы подключаются к другим элементам схемы чаще всего через микропо-лосковую линию. На рис. 11.6 показаны варианты включения полоскового резонатора по схеме двух- и четырехполюсника. Размеры зазоров s, s1, s2и длины участков взаимодействия резонатора с линией l1 и l2 выбираются, исходя из заданного коэффициента связи (коэффициента включения).
На базе прямоугольных резонаторов выполняются более сложные составные резонаторы, которые используются в конструкциях фильтров и представляют собой набор последовательно или параллельно включенных резонаторов. Пример конструкции полосового фильтра СВЧ на основе последовательно соединенных микрополосковых резонаторах приведен на рис. 11.7.
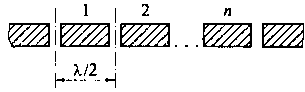
Рис. 11.7. Конструкция полосового фильтра СВЧ на основе последовательно соединенных микрополосковых резонаторов
Короткие отрезки полосковых линий с длиной l < λ/8, где λ — длина волны в линии, обладают свойствами реактивных элементов и применяются для формирования колебательных контуров в полосковых схемах.
Отрезок линии длиной l с волновым сопротивлением Wможет быть представлен эквивалентной схемой замещения T-типа участка длинной линии, приведенной на рис. 11.8 (сравните с рис. 9.4, а). Параметры схемы замещения L и С связаны с параметрами участка линии при условии l < λ/8 следующими соотношениями: L= Wl/(fλ) и С = l/(Wfλ). Потери в коротких линиях малы и обычно не учитываются.
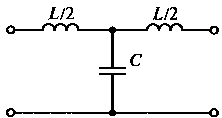
Рис. 11.8. Схема замещения Т-типа участка длинной линии
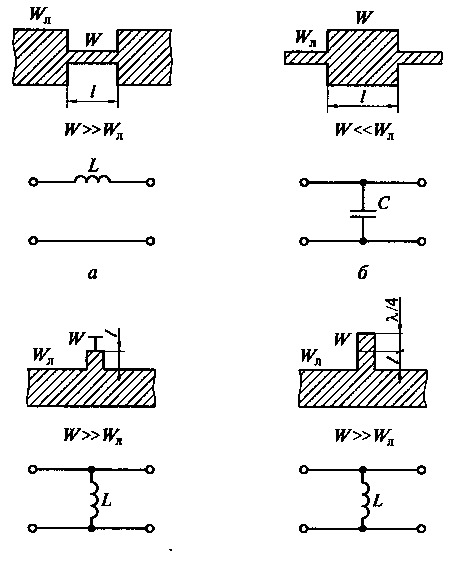
На рис. 11.9 показана конструктивная реализация реактивных элементов с помощью коротких отрезков полосковых линий длиной l < λ/8.
в г
Рис. 11.9 Конструктивная реализация реактивных элементов с помощью коротких отрезков полосковых линий длиной l < λ/8: а - последовательная индуктивность; б — параллельная емкость; в, г — параллельная индуктивность
Короткий отрезок линии передачи с весьма высоким волновым сопротивлением W, включенный в разрыв линии с более низким волновым сопротивлением Wл, эквивалентен включенной последовательно индуктивности (см. рис. 11.9, а). Соответственно, отрезок с малым волновым сопротивлением, включенный в разрыв линии с высоким волновым сопротивлением, будет вести себя как емкость, включенная в линию параллельно (см. рис. 11.9, б).
Индуктивность, включенная параллельно в линию передачи, реализуется параллельным подключением к основной линии короткозамкнутого отрезка с высоким волновым сопротивлением (см. рис. 11.9, в). Короткие отрезки линий, включаемые параллельно в основную линию передачи, называются шлейфами. В некоторых случаях для того, чтобы обойти технологические трудности создания короткозамыкающего контакта, индуктивные коротко замкнутые шлейфы с длиной l заменяют разомкнутыми шлейфами с длиной l + λ/4 (см. рис. 11.9, г).
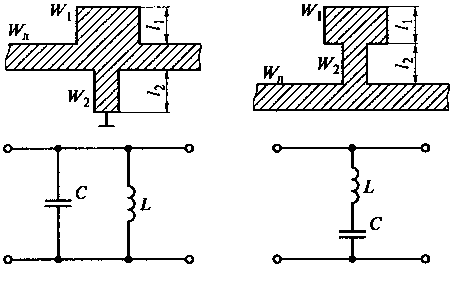
С помощью различных комбинаций короткозамкнутых и разомкнутых шлейфов можно создать полосковые структуры, эквивалентные последовательному и параллельному контуру, включенным параллельно в линию передачи. На рис. 11.10 показаны топология и эквивалентные схемы полосковых шлейфовых структур для параллельного и последовательного колебательных контуров. Полосковые шлейфовые структуры широко используют для реализации многозвенных фильтров СВЧ.
аб
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.