Для уменьшения величины модовой дисперсии применяют многомодовые градиентные световоды (рис. 10.17), в которых показатель преломления сердцевины изменяется вдоль радиальной координаты r по нелинейному закону. Траектории лучей в неоднородной среде сердцевины являются криволинейными.
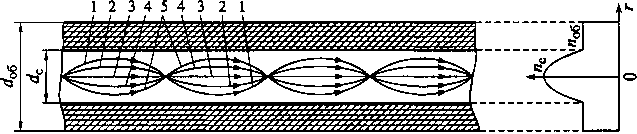
Рис. 10.17. Ход лучей и распределение показателя преломления в градиентном многомодовом ВС
На рис. 10.17 показан ход лучей и распределение показателя преломления в градиентном многомодовом ВС. Траектории лучей, пересекающих ось сердцевины под большими углами, имеют большую длину, однако они проходят в области сердцевины, где показатель преломления меньше, а фазовая скорость волн выше. Это приводит к выравниванию времен распространения различных мод в ВС, что существенно снижает величину модовой дисперсии. Лучшие образцы градиентных многомодовых ВС имеют коэффициент широ-кополосности более 1,2... 1,5 ГГц • км.
ГЛАВА 11
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
11.1. Резонансные линии. Их свойства
Колебательные системы являются одними из наиболее распространенных элементов электронных схем. В частотном диапазоне, где длины электромагнитных волн намного превосходят линейные размеры элементов электронных схем, применяются колебав тельные системы с сосредоточенными параметрами. Они реализуются в виде колебательных контуров, представляющих последовательное или параллельное соединение сосредоточенных индуктивностей, емкостей и сопротивлений. Колебательный процесс в контуре представляет непрерывный, периодический обмен энергией между электрическим полем, сосредоточенным в конденсаторе, и магнитным полем катушки индуктивности.
С повышением частоты уменьшается длина волны и соответственно должны уменьшаться размеры элементов колебательных систем с сосредоточенными параметрами. На частотах выше нескольких сотен мегагерц они становятся настолько малыми, что возникают серьезные трудности при их изготовлении и применении. Кроме того, с ростом частоты в сосредоточенных элементах увеличиваются тепловые потери (за счет скин-эффекта) и потери на излучение. Поэтому на достаточно высоких частотах (на дециметровых и более коротких волнах) применяют преимущественно колебательные системы из элементов с распределенными параметрами. Характерными примерами таких систем являются короткие отрезки длинных линий, называемые резонансными линиями, и полые резонаторы, образованные замкнутыми металлическими оболочками.
Резонансными линиями называются короткие отрезки длинных линий, которые используются в качестве колебательных контуров с распределенными параметрами. Достоинствами резонансных линий являются высокие электрические показатели, эксплуатационная надежность и простота конструкции. Применяются они в основном на дециметровых и сантиметровых волнах, так как в метровом диапазоне они приобретают недопустимо большие размеры.
Основанием для использования отрезков длинной линии в качестве колебательных систем является характер зависимости входного сопротивления линии от ее длины в режиме стоячих волн. Входное сопротивление идеальной разомкнутой линии, длина которой равна четному числу четвертей длины волны, согласно выражению (9.15) и рис. 9.16 равно бесконечности. При небольшом укорочении линии или при понижении частоты ее реактивное входное сопротивление приобретает индуктивный характер, а при незначительном увеличении длины линии или частоты — емкостной характер. Поведение линии такой длины с изменением частоты аналогично поведению параллельного колебательного контура.
Если длина разомкнутой линии равна нечетному числу четвертей длины волны, то ее входное сопротивление становится равным нулю. Поведение такой линии при незначительном изменении частоты аналогично поведению последовательного колебательного контура (см. рис. 9.15).
Зависимость входного сопротивления от длины идеальной короткозамкнутой линии имеет тот же характер, что и для разомкнутой линии, но отличается сдвигом на четверть длины волны (см. рис. 9.18, а). Поэтому короткозамкнутая линия с изменением частоты ведет себя как параллельный контур при длине, равной нечетному числу четвертей длины волны, и как последовательный контур — при длине, равной четному числу четвертей длины волны.
Отмеченные свойства отрезков линий широко используются в электронных схемах для дециметровых и сантиметровых волн. Так, линии с длиной, кратной четверти длины волны, используются в качестве колебательных контуров и согласующих трансформаторов. Отрезки линий с длиной, не кратной четверти длины волны, применяются в качестве реактивных сопротивлений.
Входное сопротивление разомкнутой и короткозамкнутой линии с потерями имеет конечные по величине активную и реактивную составляющие (см. рис. 9.16 и 9.18, б). В этом случае поведение указанных отрезков длинной линии эквивалентно поведению реальных колебательных контуров с потерями.
При рассмотрении резонансных линий отметим еще одно полезное свойство четвертьволнового отрезка разомкнутой линии (четвертьволнового трансформатора). Так как для этого отрезка справедливо соотношение Zвх Zн = Wтр2, то при активном характере волнового сопротивления трансформатора Wтрпроизведение Zвх Zн тоже должно быть активным. Это означает, что при реактивном значении Zн сопротивление Zвх тоже будет реактивным, но противоположного характера. Следовательно, четвертьволновый трансформатор не только меняет величину сопротивления нагрузки, но и изменяет его характер или, как говорят, инвертирует нагрузку (преобразует индуктивную нагрузку в емкостную, и наоборот).
Резонансные линии, соответствующие последовательному или параллельному колебательному контуру, принято характеризовать эквивалентными параметрами этого контура, к которым относятся резонансные частоты, характеристическое сопротивление, резонансное сопротивление и добротность. Эти параметры позволяют проводить расчеты электронных схем, в составе которых используются резонансные линии, точно так же, как и с применением колебательных контуров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.