Если групповой сигнал распространяется в средах или направляющих системах без дисперсии, то все его гармонические составляющие имеют одинаковую фазовую скорость, равную скорости света, и, следовательно, при распространении не изменяют взаимного расположения. В результате при распространении огибающая группового сигнала сохраняет свою форму (в средах и системах без потерь) и перемещается с той же скоростью, что и каждая из его гармонических составляющих. В этом случае групповая скорость волн совпадает с их фазовой скоростью, т.е. со скоростью света. Такая ситуация характерна для распространения T-волн в линиях передачи, если параметры ε и μ используемых в них диэлектрических сред не зависят от частоты.
В полых металлических волноводах ситуация иная, так как в них имеется внутри- и межмодовая дисперсии. Кроме того, если диэлектрическая среда, заполняющая волновод, характеризуется частотнозависимыми проницаемостями ε(ω) и μ(ω), то к внутри- межмодовой дисперсиям добавляется материальная дисперсия, приводящая к различию фазовых скоростей гармонических составляющих группового сигнала. При прохождении ими по волноводу пути длиной l они приобретают разные пространственные фазовые сдвиги. При суммировании этих составляющих в конце пройденного отрезка они образуют групповой сигнал, отличающийся от исходного. Следовательно, в результате дисперсии форма группового сигнала исказится.
При сильном искажении может произойти потеря информации, переносимая сигналом. В линиях передачи с малыми потерями дисперсия является основным фактором, ограничивающим длину участка линии без регенерации (восстановления формы) сигнала.
В волноводах быстрых волн групповая и фазовая скорости связаны соотношением: VвVгр= Vф2, показывающим, что для быстрых волн в волноводе групповая скорость меньше скорости света. С ростом частоты различие между скоростями Vв и Vгр уменьшается и обе они стремятся к скорости света Vф.
Материальная дисперсия является единственным видом дисперсии, которая наблюдается в волноводах с Т-волнами, диэлектриком в которых служит отличная от воздуха среда. Однако в высокочастотных диэлектриках, применяемых в линиях передачи, величина материальной дисперсии незначительна, поэтому длина пассивных участков линий передачи с Т-волнами ограничивается частотной зависимостью потерь в линиях, которые с ростом частоты увеличиваются, приводя к искажению формы широкополосных сигналов.
Заметим, что длина волны моды в прямоугольном волноводе, как и в любом полом металлическом волноводе, на основании (10.5) имеет две особенности:
1) она зависит от критической длины волны моды;
2) она больше длины волны λ-колебаний, возбуждаемых генератором в безграничной среде.
Характеристическое сопротивление волноводной моды определяется как отношение комплексных амплитуд ортогональных между собой поперечных компонентов электрического и магнитного полей этой моды, т.е. WE,H = Ех/Ну = -Ёу/Нх . Формулы (10.6) показывают, что с изменением длины волны поведение характеристических сопротивлений Е- и Н-волн подобно поведению фазовой и групповой скоростей волн. Для любой длины волны справедливо соотношение WH > WE. С уменьшением длины волны λ оба характеристических сопротивления стремятся к характеристическому сопротивлению плоской Т-волны в безграничном пространстве WT = 120π√μ/ε. При увеличении длины волны λ разница между характеристическими сопротивлениями WHи WEвозрастает, резко увеличиваясь при приближении λ к значению λ кр. При λ > λ кр оба сопротивления становятся мнимыми. Это означает, что между поперечными компонентами электрического и магнитного полей существует сдвиг фаз 90°. Эти компоненты, так же как ток и напряжение в длинной линии, определяют мощность электромагнитного поля, переносимую волной по волноводу. Наличие между ними фазового сдвига в 90° означает отсутствие переноса мощности. Такая ситуация соответствует наличию в волноводе стоячей волны. Это полностью согласуется с полученными ранее выводами, так как при λ > λкр реализуется запредельный режим работы волновода, при котором в нем существует стоячая волна.
Процессы в волноводах подчиняются основным положениям общей теории длинных линий. При этом для решения вопросов согласования волновода с нагрузкой или с другим волноводом используются характеристические сопротивления WHи WE. На основании формул (10.3) и (10.6) находим выражение для характеристического сопротивления основной моды Н10 прямоугольного волновода:
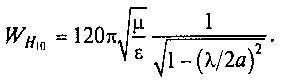
Данное выражение не зависит от размера узкой стороны волновода b. Это может привести к ложному выводу, что два волновода с одинаковыми размерами широкой стороны а могут быть согласованы независимо от размеров их узкой стороны (высоты) b. Реально же при соединении двух волноводов с различной высотой bнаблюдаются большие отражения. Это указывает на ограниченность применения понятия характеристического сопротивления моды Н10 для решения задач согласования волновода с нагрузкой.
Круглый волновод. На рис. 10.11 показаны круглый волновод радиусом Rв цилиндрической системе координат и секторы периодичности электромагнитного поля по углу φ. Волновые процессы в круглом волноводе (см. рис. 10.6, б) удобно рассматривать в цилиндрической системе координат (r, φ, z), приведенной на рис. 10.11, а. В этой системе координат поперечные компоненты поля подразделяются на радиальные Еr Нrи угловые Еφ Нφ. В заданной точке М поперечного сечения волновода радиальные компоненты направлены вдоль радиуса-вектора, а угловые — по касательной к окружности с центром в начале координат, проходящей через эту точку.
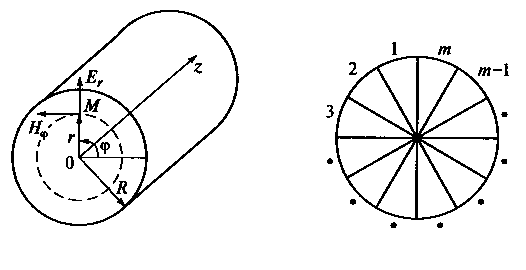
аб
Рис. 10.11. Круглый волновод радиусом Rв цилиндрической системе координат (а); секторы периодичности электромагнитного поля по углу φ (б)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.