Проектирование роботов и робототехнических систем, страница 9

 Н.

Время движения руки манипулятора найдем по формуле:

,                                                                                            (3.3)

где     – ход руки манипулятора, м, ;

 – скорость движения руки манипулятора, м/с, ;

 с.

Инерционное ускорение , м/с², вычислим по формуле:

,                                                                                        (3.4)

где     – скорость движения руки манипулятора, м/с;

 – время разгона руки, с, ;

 м/с².

Силу трения  , Н, вычислим по формуле:

,                                                                                     (3.5)

где    – коэффициент трения (сталь – сталь), ;

 – сила тяжести манипулятора, Н.

Силу трения  , Н, вычислим по формуле:

,                                                                                     (3.6)

где    – коэффициент трения (сталь – сталь), ;

 – сила тяжести манипулятора, Н.

Силу тяжести  , Н, вычислим по формуле:

,                                                                                       (3.7)

где     – ускорение свободного падения, м/с², .

 Н;

 Н;

 Н.

3.2.2 Проектный расчёт передачи

Диаметр винта D_в находим из условия прочности винта при растяжении (сжатии):

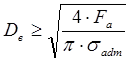,                                                                               (3.8)

где  s_аdm – допускаемое напряжение при растяжении (сжатии) винта (сталь 45), s_аdm=167 МПа.

мм.

Винт является длинным и работает на сжатие. Необходимо проверить винт на устойчивость, то есть проверить гибкость винта λ.

Условие устойчивости:

,                                                                                          (3.9)

Вычислим начальную гибкость:

,                                                                                (3.10)

где     a – эмпирический коэффициент, для сталь 45 a = 464;

b – эмпирический коэффициент, для сталь 45 b = 3,62;

 - предел текучести, для сталь 45,  3,5 МПа.

Находим минимальный возможный диаметр D_в:

 

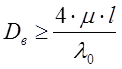,                                                                              (3.11)

где     μ – коэффициент приведения длины = 1;

l –длина винта = 1,4 м;

.

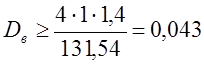Округлим значение до ближайшего стандартного, примем D_в = 50 мм.

Диаметр шариков d_ш, получим из выражения:

,                                                                   (3.12)

по формуле 3.12 получим:

 мм.

Полученный результат диаметра шарика увеличим до 10 мм, так как нам потребуется большая линейная скорость гайки, а, следовательно, шаг должен быть большой.

Определим шаг резьбы:

,                                                                      (3.13)

по формуле 3.13 получим:

мм.

Примем шаг винта 20 мм.

Определим новые диаметры шариков

Диаметр окружности, на которой располагаются центры шариков D_ср, получим из выражения:

,                                                                            (3.14)

по формуле 3.14 получим:

Наружный диаметр D_н, получим из выражения:

,                                                                   (3.15)

где     Δ – радиальный зазор, Δ = 0,03…0,12 мм.

Получим:

Угол подъёма винтовой линии ψ, получим из выражения:

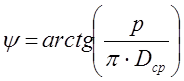,                                                                    (3.16)

по формуле 3.16 получим:

 рад.

Число шариков в рабочей части резьбы z_ш, получим из выражения:

,                                                                    (3.17)

где     z – число витков в одной замкнутой рабочей цепочке, z = 2.

по формуле 3.17 получим:

Полученное значение округлим до ближайшего меньшего целого числа, принимаем z_ш = 37.

3.2.3 Определение размеров гайки.

Число замкнутых цепочек в гайке u найдём из условия (при этом учтём, что cos ψ ≈ 1, так как угол ψ мал):

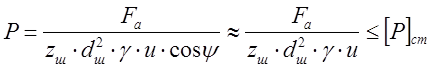,                           (3.18)

где     P – удельная осевая нагрузка, МПа;

γ = 0,8 – коэффициент неравномерности распределения нагрузки между шариками;

[P]_ст – допускаемая удельная осевая статистическая нагрузка, МПа.

[P]_ст определяют в зависимости от относительного радиального зазора χ, который вычислим по формуле: