Проектирование роботов и робототехнических систем, страница 13

, с.                                                                        (1.6)

где     n - общее число движений при прохождении между точками.

Расчет общего времени рабочего цикла для оценки быстродействия робота данной компоновки:

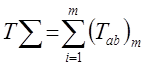, с.                                                                        (1.7)

где     m – количество перемещений.

Погрешность при линейном перемещении имеет постоянный характер и не зависит от величины перемещения.

Погрешность при угловом перемещении выражена в миллиметрах отклонения ЗУ (захватного устройства) манипулятора в заданной точке перемещения от радиуса траектории перемещения, выраженного в метрах. Графическое представление угловой погрешности изображено на рисунке (А.1).

Рисунок А.1 – Иллюстрация угловой погрешности.

У формулы 1.2 есть некоторая погрешность, но ей можно пренебречь, так как мы будем использовать ее для значении радиусов перемещений, не превышающих 3 метров.

1.2 Расчёт полярной цилиндрической компоновки

1.2.1 Ошибка позиционирования вычисляется по формулам 1.1, 1.2 и 1.3.

а) ошибка позиционирования 1-2 по:

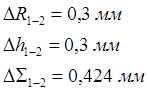, б) время перемещения по формуле 1.6:

.

1.2.2 Ошибка позиционирования и время  движения.

а) ошибка позиционирования 2-3-4:

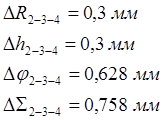, б) время перемещения по формуле 1.6:

,

1.2.3 Ошибка позиционирования и время  движения.

а) ошибка позиционирования 4-5-6:

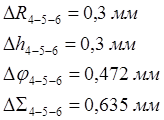, б) время перемещения по формуле 1.6:

.

1.2.4 Ошибка позиционирования и время  движения.

а) ошибка позиционирования 6-7-8:

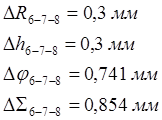, б) время перемещения по формуле 1.6:

.

1.2.5 Ошибка позиционирования и время  движения.

а) ошибка позиционирования 8-9-10:

, б) время перемещения по формуле 1.6:

.

1.2.6 Ошибка позиционирования и время  движения.

а) ошибка позиционирования 10-1:

,

б) время перемещения по формуле 1.6:

1.2.7 Общее время цикла вычисляется по формуле 1.7

1.3 Расчёт компоновки робота в декартовой системе координат

1.3.1 Ошибка позиционирования вычисляется по формулам 1.1, 1.2 и 1.3. Время  движения вычисляются по формулам 1.4, 1.5 и 1.6.

а) ошибка позиционирования 1-2-3:

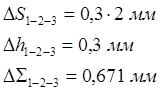, б) время перемещения по формуле 1.6:

1.3.2 Ошибка позиционирования и время движения.

а) ошибка позиционирования 3-4:

,

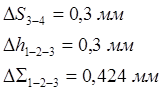б) время перемещения по формуле 1.6:

1.3.3 Ошибка позиционирования и время движения.

а) ошибка позиционирования 4-5-6:

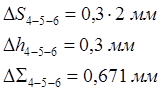, б) время перемещения по формуле 1.6:

1.3.4 Ошибка позиционирования и время движения а) ошибка позиционирования 6-7-8:

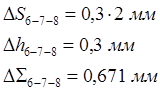, б) время перемещения:

1.3.5 Ошибка позиционирования и время движения а) ошибка позиционирования 8-9:

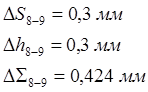, б) время перемещения по формуле 1.6:

1.3.6 Ошибка позиционирования и время движения а) ошибка позиционирования 9-1:

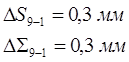, б) время перемещения по формуле 1.6:

1.3.7 Общее время цикла вычисляется по формуле 1.7:

1.4 Расчёт компоновки робота в сферической системе координат

1.4.1 Расчёт для точности позиционирования схвата

Координаты схвата:

,                                                     (1.8)

Выражения для ошибок позиционирования запишем в приращениях обобщённых координат:

                                                                                                     (1.9)

где     ΔL – линейная погрешность перемещения, ΔL = Δ_пр.

1.4.2 Ошибка позиционирования и время движения 1-2-3-4-5

а) Подставив координаты точки в уравнения схвата (1.9) и решив их, найдём значения обобщённых координат.

Координаты: X = -2,4 м; Y = -1,6 м; Z = 1,1 м;

Значения обобщённых координат:

α = 214°; β = -2°; l = 2886 мм

Значения погрешностей по каждой из осей:

ΔX = 0,052 мм

ΔY = 0,163 мм

ΔZ = 0,094 мм

Среднее значение погрешности:

мм,

б) время перемещения по формуле 1.6:

1.4.3 Ошибка позиционирования и время движения 5-6-7-8-9

а) Подставив координаты точки в уравнения схвата (1.9) и решив их, найдём значения обобщённых координат.

Координаты: X = -2,4 м; Y = 0 м; Z = 1,2 м;

Значения обобщённых координат:

α = 180°; β = 0°; l=2400 мм.

Значения погрешностей по каждой из осей:

ΔX = 0 мм

ΔY = 0,113 мм