Другие предметы \ Основы теории криптографии и криптоанализа

Учбово-методичний посібник для виконання лабораторних робіт з дисципліни „Основи теорії криптографії і криптоаналізу”, страница 14

Цей метод зменшує кількість операцій, у середньому, до 1,5k операцій, де k – довжина числа х у бітах. Знайти спосіб обчислення з найменшою кількістю операцій – важка проблема (було доведено, що послідовність повинна містити не менше k – 1 операцій), але неважко знизити число операцій до 1,1k.

1.3.2.  Прості числа

Визначення 3.2.1. Число р ÎN, р ¹1, називається простим, якщо р має в точності два позитивних дільника: 1 і р. Інші натуральні числа (крім 1) прийнято називати складеними. Число 1 – ні просте, ні складене. [11]

Два – це просте число. Простими є і 73, 2521, 2365347734339 і 2756839–1. Криптографія, особливо криптографія з відкритими ключами, часто використовує великі прості числа (512 біт і навіть більше).

Відзначимо деякі властивості, зв'язані з простими числами.

Властивість 3.2.1. Найменший дільник будь-якого числа а ÎN, відмінний від 1, є число просте. [11]

Доказ. Нехай с|а, з ¹1 і c – найменше з цією властивістю. Якщо існує c1 таке, що c1|с, то c1£с і c1|а, отже, c1=c або c1=1.

Властивість 3.2.2. Найменший відмінний від 1 дільник складеного числа а ÎNне перевершує . [11]

Доказ. с|а, c ¹ 1, c – найменший, отже а = са1, а1|а, а1 ³ с, значить аа1 ³ с2а1, а ³с2 і c £.

Теорема 3.2.1. Простих чисел нескінченно багато. [11]

Доказ. Від противного. Нехай р1, р2,..., рn – усі прості. Розглянемо число а = р1р2...рn+1. Його найменший відмінний від 1 дільник c, будучи простим, не може збігатися з жодним з р 1, р 2,..., р n, тому що інакше с|1.

Для складання таблиці простих чисел древній грек Ератосфен придумав процедуру, що одержала назву "решето Ератосфена":

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,...

Йдемо по натуральному ряду. Підкреслюємо перше непідкреслене і невикреслене число, а з подальшого ряду викреслюємо кратні тільки що підкресленому. І так багато разів. Легко зрозуміти, що підкреслені числа – прості. Якщо згадати властивість 2, то стає зрозуміло, що коли викреслено всі кратні простих, менших р, то всі, що залишились невикресленими, менші р2 – прості. Це значить, що складання таблиці всіх простих чисел менших N закінчено відразу, як тільки викреслені всі кратні простих, менших .

В даний час складені таблиці всіх простих чисел, що не перевершують 50 мільйонів, далі відомі тільки окремі їхні представники. [1]

Найважливішою і загальновідомою в цьому пункті є наступна теорема. Ця теорема зветься "Основна теорема арифметики".

Теорема 3.2.2. Усяке ціле число, відмінне від -1, 0 і 1, єдиним чином (з точніс­тю до порядку співмножників) можна розкласти в добуток простих чисел. [11]

Доказ. Будемо доводити твердження теореми тільки для натуральних чисел.

Нехай а >1, р1 – його найменший простий дільник. Виходить,

а = р1а1. Якщо, далі, а1 >1, то нехай р2 – його найменший простий дільник і а1 = р2а2, тобто а = р1р2а2, і так далі, поки аn не стане дорівнювати одиниці. Це обов'язково відбудеться, тому що а >а1 >а2... Маємо, таким чином,

a = p1p2...pn, і можливість розкладання доведена.

Покажемо одиничність. Нехай a = q1q2...qn – інше розкладання, тобто p1p2...pn = q1q2...qs. В останній рівності права частина поділяється на q1, отже, ліва частина поділяється на q1. Покажемо, якщо добуток p1p2...pn поділяється на q1, тоді один зі співмножників рk зобов'язаний поділятися на q1.

Дійсно, якщо q1|p1, то усе доведено. Нехай q1 не поділяє p1. Тому що q1 – просте число, то (q1, p1) = 1. Тому знайдуться такі u, v ÎZ, що up1+vq1 = 1. Помножимо останню рівність на p2...pn, одержимо: p2...pn =p1(p2...pn) u+q1(p2...pn) v. Обоє додатків праворуч поділяються на q1, отже, p2...pn поділяється на q1.

Тепер нехай, наприклад, q1|p1. Значить q1=p1, тому що p1 – просте. З рівності p1p2...pn =q1q2...qs скороченням одержимо рівність p2...pn =q2...qs. Знову міркуючи по індукції, бачимо, що n = s, і кожен співмножник лівої частини рівності p1p2...pn =q1q2...qn обов'язково є присутнім у правій і навпаки.

Відразу відзначимо без доказу два досить очевидних наслідки з цієї теореми.

Наслідок 3.2.1. Усяке раціональне число можна однозначно представити у вигляді:

де a1, a2,..., ak ÎZ. [11]

Наслідок 3.2.2. Якщо

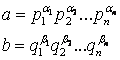 – цілі числа, то найбільший загальний дільник a і b дорівнює ,

а найменше загальне кратне a і b дорівнює

де gi = min{ai,bi}, adi = max {ai,bi}. [11]

1.3.3.  Найбільший загальний дільник

Визначення 3.3.1. Число d ÎZ, що поділяє одночасно числа а, b, c,..., k ÎZ, називається загальним дільником цих чисел. Найбільше d з такою властивістю називається найбільшим загальним дільником. Позначення: d = (a, b, c,..., k). [11]

Перелічимо основні властивості найбільшого загального дільника.

Властивість 3.3.1. Якщо (a, b) = d, то найдуться такі цілі числа u і v, що d = au+bv. [11]

Властивість 3.3.2. Для будь-яких цілих чисел а і k справедливо:

(а, kа) = а; (1, а) = 1. [11]

Властивість 3.3.3. Якщо a = bq + c, то сукупність загальних дільників a і b збігається із сукупністю загальних дільників b і c, зокрема,

(a, b) = (b, c). [11]

Доказ. Нехай d|a, d|b, тоді d|c. Нехай d|c, d|b, тоді d|a.

Якщо d ціле число раз укладається в а и в b, то, мабуть, що d зобов'язано ціле число раз укластися й у с.

Властивість 3.3.4. Нехай a, b і m – довільні цілі числа. Тоді

(am, bm) = m×(a, b). [11]

Доказ. Якщо d – найбільший загальний дільник чисел а і b, то dm|am і dm|bm, тобто dm – дільник am і bm. Покажемо, що dm – найбільший загальний дільник цих чисел. Оскільки d – найбільший загальний дільник чисел а і b, то, відповідно до властивості 3.3.1., для деяких цілих чисел u і v виконується рівність d = au + bv. Помноживши цю рівність на m, одержимо рівність:

dm = amu+bmv.

Видно, якщо деяке число s поділяє одночасно am і bm, то s зобов'язано поділяти і dm, тобто s £dm, отже, dm – найбільший загальний дільник.

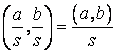Властивість 3.3.5. Нехай s – дільник а і b. Тоді:

 [11]

Доказ.

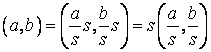
Властивість 3.3.6. Очевидно тепер, що

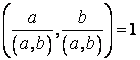 [11]

Властивість 3.3.7. Якщо (a, b) = 1, то (ac, b) = (c, b). [11]

Скачать файл