Інший, більш простий тест був незалежно розроблений Леманном (Lehmann). [6] От послідовність дій при перевірці простоти числа p:
1. Виберіть випадкове число a, менше p.
2.
Обчислите 
.
3.
Якщо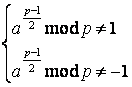 
, то p не
є простим.
4.
Якщо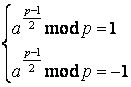 
, то
імовірність того, що число p не є простим, не більше 50 відсотків.
І знову, імовірність того, що випадкове число a буде свідком складеної природи числа p, не менше 50 відсотків. Повторіть цю перевірку t раз. Якщо результат обчислень дорівнює 1 або -1, але не завжди дорівнює 1, то p є простим числом з імовірністю помилки 1/2t.
Приведемо алгоритм мовою C++, тестуючий число p на простоту, задану кількість разів:
bool Lehmann_Test(unsigned long Iterations, unsigned long p)
{
Randomize();
unsigned long a=0;
for(unsigned long i=1;i<=Iterations;i++)
{
a=RandomRange(2,p);
if((PowerMod(a,(p-1)/2,p)!=1)&&(PowerMod(a,(p-1)/2,p)!=p-1))return false;
}
return true;
}
Тут функція PowerMod реалізує зведення в ступінь по модулю.
Тест Рабіна-Міллера
Повсюдно використовуваним є простий алгоритм, розроблений Майклом Рабіном (Michael Rabin), частково заснованим на ідеях Гарі Міллера. По суті, це спрощена версія алгоритму, рекомендованого в стандарті DSS. [10]
Виберіть для перевірки випадкове число p. Обчисліть b – число розподілів p – 1 на 2 (тобто, 2b – це найбільший ступінь числа 2, на яке поділяється p – 1). Потім обчислите m, таке що p = 1+2b× т.
1. Виберіть випадкове число a, менше p.
2. Установіть j = 0 і z = am mod p.
3. Якщо z = 1 або якщо z =p – 1, то p проходить перевірку і може бути простим числом.
4. Якщо j >0 і z = 1,то p не є простим числом.
5. Установіть j = j+1. Якщо j < b і z ≠ p – 1, установіть z = z2 mod p і поверніться на етап 4. Якщо z =p – 1, то p проходить перевірку і може бути простим числом.
6. Якщо j = b і z ≠ p – 1, то p не є простим числом.
У цьому тесті імовірність проходження перевірки складеним числом знижується швидше, ніж у попередньому. Гарантується, що три чверті можливих значень a виявляться свідками. Це означає, що складене число пройде через t перевірок з імовірністю не більшої 1/4t, де t – це число ітерацій. Насправді і ці оцінки занадто песимістичні. Для більшості випадкових чисел близько 99,9 відсотків можливих значень а є свідками. [1]
Існують більш точні оцінки.
Для n-бітового кандидата в прості числа (де п більше 100),
імовірність помилки в одному тесті менше, ніж 1 на 
.
І для 256-бітового n імовірність помилки в шести тестах менше, ніж 1/251.
Приведемо алгоритм мовою C++ що перевіряє задану кількість разів, чи є число p простим:
bool Rabin_Miller_Test(unsigned long Iterations,unsigned long p)
{
unsigned long b=0;
unsigned long m=p-1;
while(m%2==0)
{
b++;
m=m>>1;
}
Randomize();
unsigned long a=0;
unsigned long j=0;
unsigned long z=0;
for(unsigned long i=1;i<=Iterations;i++)
{
a=RandomRange(2,p);
j=0;
z=PowerMod(a,m,p);
if((z==1)||(z==(p-1)))return true;
while((j<b)&&(z!=(p-1)))
{
if((j>0)&&(z==1))return false;
j++;
z=PowerMod(z,2,p);
}
if((j==b)&&(z!=(p-1)))return false;
}
return true;
}
Практичні рекомендації з генерації простих чисел
У реальних програмних пакетах генерація простих чисел відбувається швидко:
1. Згенеруйте випадкове n-бітове число p.
2. Установіть старший і молодший біти рівними 1. (Старший біт гарантує необхідну довжину простого числа, а молодший біт забезпечує його непарність.)
3. Переконайтесь, що p не поділяється на невеликі прості числа: 3, 5, 7, 11, та ін. У багатьох реалізаціях перевіряється подільність р на всі прості числа, менші 256. Найбільш ефективною є перевірка на подільність для всіх простих чисел, менших 2000.
4. Виконайте тест Рабіна-Міллера для деякого випадкового a. Якщо p проходить тест, згенеруйте інше випадкове a і повторіть перевірку. Вибирайте невеликі значення a для прискорення обчислень. Виконаєте п'ять тестів. Якщо p не проходить однієї з перевірок, згенеруйте інше p і спробуйте знову.
Інший шлях – можна не генерувати p випадковим чином щоразу, але послідовно перебирати числа, починаючи з випадково обраного доти, поки не буде знайдене просте число. [6]
Етап 3 не є обов'язковим, але це гарна ідея. Перевірка, що випадкове непарне р не поділяється на 3, 5 і 7 відтинає 54 відсотка непарних чисел ще до етапу 4. Перевірка подільності на всі прості числа, менші 100, забирає 76 відсотків непарних чисел, перевірка подільності на всі прості числа, менші 256, забирає 80 відсотків непарних чисел. У загальному випадку, частка непарних кандидатів, що не поділяються на жодне просте число, менше n, дорівнює 1,12/ln n. Чим більше n, тим більше попередніх обчислень потрібно виконати до тесту Рабіна-Міллера.
Якщо n – добуток двох простих чисел, p і q, то може знадобитися використовувати в якості p і q сильні прості числа. [1] Такі прості числа володіють рядом властивостей, що ускладнюють розкладання добутку п визначеними методами розкладання на множники. Серед таких властивостей були запропоновані:
- Найбільший загальний дільник p – 1 і q – 1 повинні бути невеликими.
- Числа р – 1 і q – 1 повинні мати серед своїх множників великі прості числа, відповідно р' і q'.
- Числа р – 1 і q – 1 повинні мати серед своїх множників великі прості числа.
- Числа р + 1 і q + 1 повинні мати серед своїх множників великі прості числа.
- Числа (р–1)/2 і (q–1)/2 повинні бути простими. (Зверніть увагу, при виконанні цієї умови виконуються і два перших.)
Як іншу односпрямовану функцію в криптографії часто використовується зведення в ступінь по модулю. Легко обчислити:
ax mod n
Задачею, зворотною зведенню в ступінь по модулю, є пошук дискретного логарифма. А це вже нелегка задача:
Знайти x, для якого ах º b (mod n).
Приклад 3.15.1. Якщо 3х º 15 (mod 17), то x = 6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.