Статистическое моделирование. Построение статистических рядов и функций, страница 12

·Математическое ожидание и дисперсия нормально распределенной случайной величины связаны с параметрами следующим образом:

·Е[ξ]=m,   V[ξ]=s².

Обозначение того, что случайная величина ξ распределена по нормальному  закону распределения с параметрами m и s следующее: ξÎN(m, s).

4. НАХОЖДЕНИЕ          ВЫБОРОЧНЫХ            ЧИСЛОВЫХ 

                                         ХАРАКТЕРИСТИК

     4.1  Числовые характеристики случайных величин

Одним из важнейших понятий теории вероятностей является понятие математического ожидания случайной величины ξ. Математическим ожиданием называют число, которое для случайной дискретной величины вычисляют по формуле:

                                    ·    ,

а для случайной непрерывной величины  по следующей формуле

                                              ·  .

Так как в определении математического ожидания принимают участие ряд и несобственный интеграл, то предполагается, что имеет место абсолютная сходимость каждого.

     Существенным предположением, на котором основано построение выборочной теории, служит основная гипотеза математической статистики, которая формулируется следующим образом:

« Все выборочные значения х₁, х₂,…, х_n, являются

· случайными величинами,

· независимыми (стохастистически)  друг от друга,

· с одинаковым распределением, совпадающим с законом распределения исходной случайной величины  ξ»

     В силу основной гипотезы можно утверждать, что выполняются условия частной теоремы Чебышева, которая утверждает, что среднеарифметическое достаточно большого числа независимых одинаково распределенных случайных величин, сходится по вероятности к их общему математическому ожиданию.

      Используя выше сформулированную теорему и, располагая выборочной статистической информацией, оценку  неизвестного математического ожидания (samplemean)  и неизвестной дисперсии (samplevariance) можно вычислить по следующим  формулам:

·     

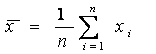
выборочное среднее.

·    ,

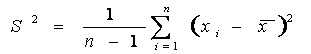выборочная  дисперсия.

Эти формулы  трансформируются в нижеприведенные, если данные представлены в виде сгруппированного ряда для дискретной случайной величины .

·         ,                        ,

· ,

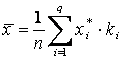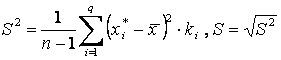    Или интервального ряда  для непрерывной случайной величины                   

·  

·

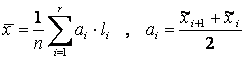
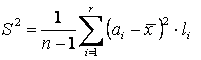
     Выборочное среднее и выборочная дисперсия, рассчитанные  по указанным формулам, будут являться несмещенными и состоятельными оценками.

     Вычисление оценки дисперсии по формулам:

                                   ·   ,