К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 17

2.2. Примеры решения задач

Задача 2.1.

         Определить положения главных центральных осей и вычислить главные центральные моменты инерции сечения (рис. 2.3).

Решение

         Найдем положение центральной оси z – z сечения. Отсчет координаты  ведем от вспомогательной оси .

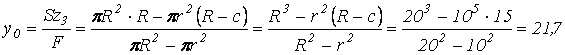 см.

         Моменты инерции фигуры относительно осей z – z и y – y найдем как разность моментов инерции большого и малого круга. Момент инерции большого круга относительно своей центральной оси :

.

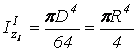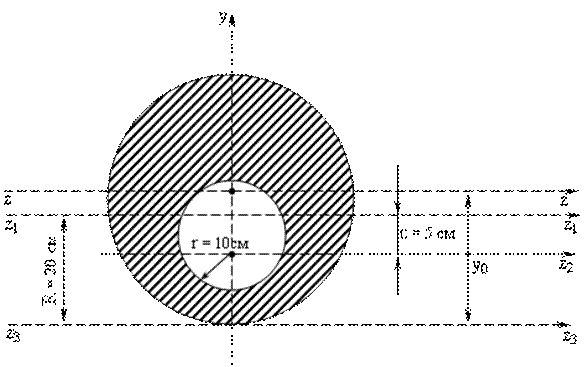
Рис. 2.3.

         Относительно оси z – z:

.

         Аналогично момент инерции малого круга относительно оси z – z:

.

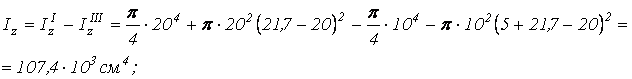
Задача 2.2.

         Найти положение главных центральных осей и вычислить главные центральные моменты инерции сечения (рис. 2.4)

Решение

         По таблице сортамента находим площадь, моменты инерции и координаты центра тяжести каждого элемента. Для швеллера №22а: , , , .

         Для уголка 100х100х10: , , , , .

         Для нахождения положения центра тяжести фигуры в качестве вспомогательных выбираем центральные оси  и  швеллера. Относительно этих осей статические моменты швеллера равны нулю, и вычисление координат центра тяжести сечения упрощается.

         Статические моменты сечения относительно осей  и :

         Площадь составного сечения:

         Координаты центра тяжести составного сечения относительно осей  и :

         Определяем осевой и центробежный моменты инерции составного сечения относительно центральных осей  и :

– для швеллера: , .

– для уголка:      , .

         Осевые моменты инерции относительно оси :