К практическим занятиям, самостоятельному изучению и выполнению контрольных и расчетно-графических работ по темам: «Растяжение и сжатие», «Геометрические характеристики плоских сечений», «Кручение», «Прямой изгиб», страница 15

где    , т.е.:

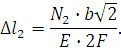
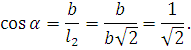
Подставим полученные значения в уравнение (2):

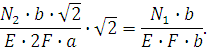
                                                                                                         (3)

         Подставим уравнение (3) в уравнение (1):

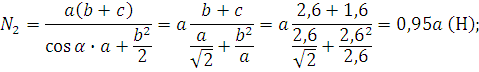
2. Определим допускаемую грузоподъемность.

Т.е.

Тогда

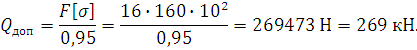
3. Определим предельную грузоподъемность системы  и

Подставим эти значения в уравнение (1):

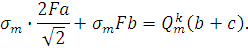
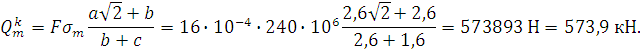
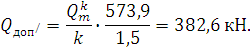
4. Сравним  и

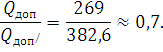
         Ответ:       

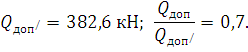
2.  Геометрические характеристики плоских сечений

2.1. Основные понятия и зависимости

К геометрическим характеристикам поперечного сечения бруса относятся: площадь, основные и полярные моменты, а также статические моменты и центробежные моменты инерции сечения.

Статические моменты плоских сечений

         Статическими моментами сечения относительно координатных осей z и y называют интегралы вида

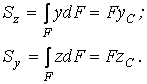
где     и  – расстояния от центра тяжести сечения соответственно до осей  и  (рис. 2.1).

Рис. 2.1

         Статический момент плоского сечения относительно любой центральной оси равен нулю.

         Моменты инерции: осевые (экваториальные), полярный и центробежный.

         а) Интегралы вида

называются осевыми или экваториальными моментами инерции сечения относительно оси z и y (рис. 2.1.).

         б) Интеграл вида

называется полярным моментом инерции сечения относительно точки О (рис. 2.1.).

         в) Интеграл вида

называется центробежным моментом инерции сечения относительно осей z и y.

Некоторые свойства моментов инерции