Методические основы построения математической модели совместного производства, страница 8

                              a_г×dF_ст,вн×(T_г – Т_ст,вн) =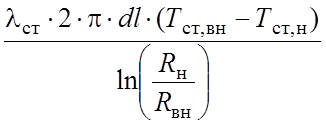          (2.60)

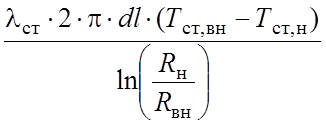                                = a_в×dF_ст,н×(T_ст,н – Т_в)    (2.61)

где dn₁ – количество метанола, образовавшегося по реакции (2.22), моль;

dn₂ – количество СО₂, прореагировавшего по реакции (2.23), моль;

      r₁ и r₂ – скорости реакций (2.22) и (2.23), моль/с;

      N – количество моль газовой смеси на входе в слой, моль;

      с_р – теплоемкость газовой смеси, Дж/(моль×К);

      dТ – изменение температуры в слое, К;

      Q₁ и Q₂ – тепловые эффекты реакций (2.22) и (2.23), Дж/моль;

      a_г – коэффициент теплоотдачи от газовой смеси к стенке трубы, Вт/(м²×К);

      a_в – коэффициент теплоотдачи от кипящей воды к стенке трубы, Вт/(м²×К);

      l_ст - коэффициент теплопроводности материала труб, Вт/(м×К);

      d_ст – толщина стенки, м;

      dF_ст,вн, dF_ст,н – внутренняя и наружная поверхности элемента трубы, соответствующего слою катализатора, м²;

       dl – высота элемента трубы, м;

       R_н и R_вн – наружный и внутренний радиусы трубы, м;

       Т_г – температура газовой смеси на входе в слой, К;

       Т_ст,вн и Т_ст,н – температуры внутренней и наружной стенок трубы, К;

       Т_в – температура воды, кипящей в межтрубном пространстве, К.

Уравнения (2.57,2.58) описывают материальный баланс в слое катализатора, уравнение (2.59) – тепловой баланс в слое, уравнения (2.60,2.61) - перенос тепла от газовой смеси к кипящей в межтрубном пространстве воде.

Подобная система уравнений предложена в [65] для адиабатического процесса синтеза  метанола в полочном реакторе. В этой работе авторы считают, что при синтезе метанола необходимо учитывать внутридиффузионное торможение, т.к. в зерне существуют градиенты концентраций и температуры.  В математических моделях это отражается введением понятия степень использования внутренней поверхности h [19,20]. Основная сложность расчета процесса на зерне состоит в надежном определении коэффициентов диффузии реагентов (напомним, что в рассматриваемом процессе газовая смесь состоит из 8 компонентов) и порядка реакции. С другой стороны, в [29] доказывается, что влияние внешне- и внутридиффузионного торможений отсутствует, поэтому реакции протекают в кинетической области. Согласно [19] процесс в пористом зерне катализатора можно считать изотермическим, т.к. интенсивность переноса тепла примерно на два порядка превышает интенсивность переноса вещества. Мы полагаем, что в нашей модели допустимо согласиться с авторами [19,29] и не рассчитывать процесс на зерне, т.е. принять h = 1. При обоснованной необходимости расчет h может быть включен в математическую модель в виде блока.

При расчете теплопередачи мы приняли следующие допущения [75,76]:

-  реактор работает в стационарном режиме;

-  потери теплоты в окружающую среду пренебрежимо малы;

-  вода в межтрубном пространстве кипит по всей высоте реактора при постоянной  температуре.

Система уравнений (2.57-2.61) решается с заменой дифференциалов на конечные разности (метод Рунге-Кутта), т.е. рассматривается конечный объем слоя Dv.

При этом появляется еще несколько допущений:

-  коэффициенты теплоотдачи постоянны на всей поверхности рассматриваемого элемента;

-  в стенке элемента трубы, соответствующего рассматриваемому слою, градиент температуры существует  только в направлении от внутренней поверхности к внешней, а по высоте температура стенки постоянна;

-  свойства смеси рассчитываются при условиях входа в слой и по высоте слоя считаются постоянными.

Погрешности, связанные с указанными допущениями, тем меньше, чем меньше разность температур на входе и выходе из слоя, которая зависит, в свою очередь, от выбранного шага по высоте трубы Dl (и, соответственно, объема Dv). Таким образом, шаг по высоте должен быть не слишком большим, чтобы разность температуры по высоте была минимальна, но и не слишком маленьким, чтобы излишне не увеличивать объем расчетов. На основании этих рассуждений мы приняли шаг по длине слоя равным 0,1 м.

Общий коэффициент теплоотдачи a_об от слоя к стенке учитывает пристенный коэффициент теплоотдачи a_ст и теплопроводность слоя. Причем [20]:

a_об = a_ст /(1 + 0,25Bi)

Согласно [20] для синтеза метанола Bi = 0,09, тогда a_об = 0,978 a_ст. Таким образом, влияние теплопроводности слоя мало и под величиной  коэффициента теплоотдачи мы понимали общий коэффициент теплоотдачи от слоя к стенке, величину его вычисляли по формулам  (2.42-2.47).

При кипении воды коэффициент теплоотдачи определяли по формуле (2.54). Удельную тепловую нагрузку находили из выражения:

                                                   q = a_г×(Т_г - Т_ст,в)                                             (2.62)

          Для каждой жидкости существует критическая тепловая нагрузка, при которой пузырьковый режим кипения переходит в пленочный, и коэффициент теплоотдачи резко падает [76]. Для воды q_кр = 1,16×10⁶ Вт/м² [48,77]. Расчет по приведенной модели показал, что в рассматриваемом нами процессе тепловая нагрузка не превышает 12500 Вт/м². Таким образом, перехода к пленочному режиму не происходит.

          Теплопроводность материала трубы определялась при температуре внутренней стенки. Это не вызывает погрешностей, т.к. по результатам расчета температуры внутренней и наружной стенок отличаются не более чем на 4 °С.

          Для вычисления m_m,ст, Pr_ст, l_ст и q  нужно до начала расчета слоя знать температуру внутренней стенки. В первом слое приняли Т_ст,вн = (Т_г + Т_в)/2. Далее определяется точное значение Т_ст,вн в первом слое, а для каждого последующего слоя для вычисления m_m,ст, Pr_ст, l_ст и q значение Т_ст,вн принимали из предыдущего слоя. При расчете по модели оказалось, что при переходе к каждому следующему слою изменение Т_ст,вн не превышает 1,5 °С, поэтому  использованный нами прием не вызвал больших погрешностей.