Методические основы построения математической модели совместного производства, страница 3

          Теплоемкость и энтальпию газовой смеси определяли по правилу аддитивности (y– мольная доля компонента) [30]:

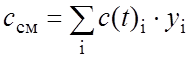                                               (2.8)

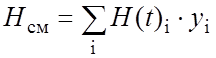                                            (2.9)

    3) вязкость и теплопроводность газов

          Вязкость m (Па×с)  и теплопроводность l (Вт/(м×К)) газов при повышенном давлении удобно определять следующим образом [59]:

                                                  m = m₀ + m_р                                                             (2.10)

                                                   l = l₀ + l_р                                                             (2.11)

где m₀ и l₀ – вязкость и теплопроводность при данной температуре, m_р и l_р – поправки на давление. Зависимость m₀ и l₀ от температуры получали аппроксимацией полиномами 2-й степени данных из [74,82]:

                                                   m₀ = f(t)                                                                                                                       l₀ = f(t)                                                          

          Поправку m_р вычисляли по методу Джосси-Стила-Тодоса, l_р – по методу Стила-Тодоса [59]. В этих методах m_р и l_р являются функциями приведенной плотности (последняя зависит от Р и t процесса). Для расчета необходимо знать критические параметры веществ. Математический аппарат можно смотреть в [59]. Сравнение расчетных значений с практическими данными из [56,59,74,82] показывает, что погрешность составляет 1-4 %.

          Вязкость m_см газовой смеси определяли по правилу Вильке [59] (формулы (1,2) Приложения III), теплопроводность смеси l_см – по методу Линдсея-Бромли (формулы (3-6) Приложения III):

    4) плотность

          Плотность газовой смеси r_см при повышенном давлении рассчитывали по правилу аддитивности:

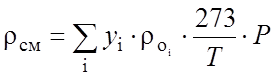                                                                                    (2.12)         Зависимость плотностей жидких воды и метанола получали аппроксимацией полиномами 2-й степени практических данных из [51]:

                                                   r_в = f(t)                                                                                                                       r_м = f(t)                                                              

    5) давление насыщенных паров

          Зависимость давления насыщенных паров воды от температуры получали аппроксимацией полиномом 2-й степени данных из [56]:

                                                   Р_нп,в = f(t)             

          Таким образом, зависимости свойств веществ и их смесей от температуры и давления мы выразили в виде полиномов различных степеней, что очень удобно при реализации математической модели на ЭВМ.

          2.4. Моделирование физико-химических процессов.

          В основе рассматриваемого комплексного производства лежат процессы, связанные с протеканием химических реакций, поэтому их формальное описание является неотъемлемой  частью модели. Также требуют рассмотрения процессы конденсации, т.к. они протекают совместно с процессами теплообмена.  Последним уделено наибольшее внимание, а особенно утилизации тепла экзотермических реакций синтеза метанола.

          2.4.1. Химические реакции.

В комплексном производстве аммиака и метанола протекают следующие реакции: 

 1)  первичный риформинг метана

                              СН₄ + Н₂О  « 3Н₂ + СО, DН = 206,4 кДж                         (2.13)

                              СО + Н₂О  « Н₂ + СО₂, DН = - 41,2 кДж                        (2.14)

                              С_nH_m + nН₂О  « nCO + (2n + m)/2 H₂, DН > 0                    (2.15)

          Гомологи метана реагируют по реакциям (2.15) до конца [74].

 2)  вторичный риформинг метана

                              О₂ + 2Н₂  « 2Н₂О, DН = - 241,7                                          (2.16)

                              СН₄ + Н₂О  « 3Н₂ + СО, DН = 206,4 кДж                               

                              СО + Н₂О  « Н₂ + СО₂, DН = - 41,2 кДж                             

          В соответствии с рекомендациями из [74] мы полагали, что сначала протекает реакция (2.16), причем кислород сгорает только с водородом, т.к. константа скорости реакции горения Н₂ значительно больше, чем СО и СН₄.

 3)  конверсия СО

                                         СО + Н₂О  « Н₂ + СО₂, DН = - 41,2 кДж                              

          Процесс осуществляется в две стадии, отличающиеся  температурой проведения реакции [77].

 4) очистка газа

          Эта стадия включает в себя очистку от СО₂ раствором моноэтаноламина согласно реакций (2.17,2.18) и тонкую очистку от СО и СО₂ методом метанирования по реакциям (2.19,2.20).

                              CO₂ + 2RNH₂ + H₂O « (RNH₃)₂CO₃                                   (2.17)

                              CO₂ + (RNH₃)₂CO₃  + H₂O « 2RNH₃HCO₃                       (2.18)

СО + 3Н₂  « СН₄ + Н₂О, DН < 0                                      (2.19) СО₂ + 4Н₂  « СН₄ + 2Н₂О, DН < 0                                        (2.20)

В балансовых расчетах количество СО₂, поглощенного раствором МЭА, вычисляли по равновесному давлению СО₂ над раствором МЭА на выходе газовой смеси из абсорбера. Равновесное давление СО₂ зависит от температуры, концентрации раствора МЭА и степени карбонизации глубокорегенерированного потока [74]. Аналитические зависимости, предложенные в [49], не дают удовлетворительных результатов, поэтому мы использовали практические данные, приведенные в [74]. В балансовых расчетов растворимостью газов в МЭА-растворе пренебрегли согласно [19]. Согласно [74] мы полагали, что реакции (2.19,2.20) необратимы.