Методические основы построения математической модели совместного производства, страница 5

          Уравнение (2.31) является общим и справедливо для любых давлений, температур и составов фаз.

Давление насыщенных паров Р_нас определяли по уравнению Антуана [59]:

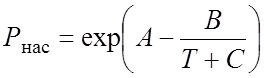                                   (2.32)

где А,В,С – коэффициенты для данного компонента; Т – температура, К; Р_нас – в мм рт. ст.

Поправка Пойнтинга была рассчитана по уравнению:

                                 

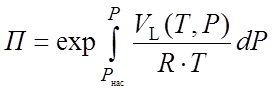
где V_L(Т,Р) – функциональная зависимость мольного объема жидкости V_L от температуры T и давления Р.

Подробнее математический аппарат можно смотреть в [59].

В программе MathCAD 2000 были рассчитаны поправки Пойнтинга для метанола и воды. Результаты расчета показали, что в диапазоне давлений 1 – 100 атм и температур 0 – 250 °С поправка Пойнтинга для метанола и воды равна единице с точностью до шестого знака после запятой.

Математический аппарат для вычисления коэффициентов фугитивности Ф громоздок и сложен, и поэтому здесь не приводится. Подробнее его можно смотреть в [59].

Для заданного состава газовой фазы в программе MathCAD 2000 были рассчитаны коэффициенты фугитивности метанола и воды. Результаты показали, что Ф для метанола и воды при 40-80 °С и 60-80 атм отличаются от единицы на 2-5 %. Однако включение блока расчета коэффициентов фугитивности в общую математическую модель требует очень сложных итерационных процедур, т.к. Ф зависит от равновесного состава газа, а последний сам зависит от Ф. Поэтому мы приняли, что без больших погрешностей можно считать Ф равными единице как для метанола, так и для воды.

Коэффициент фугитивности жидкости Ф_s в [59] рекомендуют считать его равным 1 при температурах жидкостей, значительно ниже критической. В нашем случае температура процесса 40 – 50 °С, критическая температура метанола – 239,6 °С, воды – 374,3 °С. Мы посчитали возможным принять рекомендации и не рассчитывать Ф_s.

Коэффициенты активности компонентов в жидкой фазе можно рассчитать уравнению Ван-Лаара [59] для бинарной жидкой смеси:

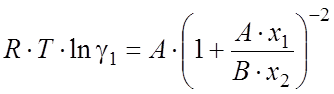                                   (2.33)

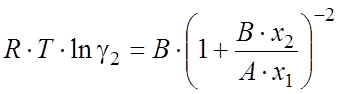                                   (2.34)

где x_i – мольные доли компонентов; A и B - так называемые настраиваемые параметры, определяемые следующим образом. При бесконечном разбавлении x₁ ® 0 или x₂ ® 0, тогда уравнения (2.33,2.34) принимают вид:

                                               (2.35)

                                               (2.36)

где g^¥ - коэффициент активности при бесконечном разбавлении, рассчитываемый по уравнению [59]:

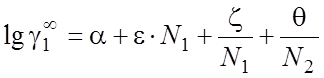                                     (2.37)

где a, e, z, q - коэффициенты для первичных спиртов, если растворитель – вода, или для воды, если растворитель – первичный спирт; N₁, N₂ – общее число углеродных атомов в молекулах 1 и 2 соответственно.

Коэффициенты a, e, z, q зависят от температуры, соответствующие табличные данные из [59] аппроксимированы полиномами 2-й степени: a = f(t), e = f(t), z = f(t), q = f(t).

С помощью пакета MathCAD 2000 рассчитали коэффициенты активности метанола и воды в их бинарном растворе. Результаты расчета приведены в таблице 1.

Таблица 1.

Результаты расчета коэффициентов активности

Температура, °С	Коэффициент активности  метанола						Коэффициент активности воды
	Мольная доля метанола  в растворе						Мольная доля воды в растворе
	0,001	0,2	0,4	0,6	0,8	0,999	0,001	0,2	0,4	0,6	0,8	0,999
20	4,036	2,172	1,464	1,161	1,034	1,000	2,767	2,074	1,587	1,262	1,069	1,000
40	4,134	2,203	1,475	1,165	1,034	1,000	2,822	2,102	1,600	1,267	1,070	1,000
60	4,367	2,253	1,487	1,167	1,035	1,000	2,878	2,142	1,624	1,279	1,073	1,000
80	4,757	2,322	1,498	1,168	1,034	1,000	2,935	2,192	1,659	1,298	1,079	1,000

          Как видно, коэффициенты активности могут очень сильно отличаться от единицы, поэтому их учет необходим для корректного расчета.

          Итак, приняв П = 1, Ф = 1, Ф_s = 1 и рассчитав g, записывали уравнение (2.31) для метанола и воды. Полученную систему уравнений необходимо решать методом итераций.

В случае конденсации только одного компонента его объем  в выходящей газовой смеси V_вых,в (нм³/ч) определяли по формуле [19]:

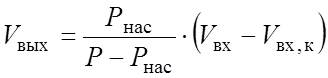                                      (2.38)

где Р_нас - давление насыщенных паров конденсирующегося компонента при заданной температуре, ата; V_вх - общий объем входящего газа, нм³/ч; V_вх,к - объем конденсирующегося компонента на входе, нм³/ч.

          Массовый расход жидкой фазы G_ж (кг/ч) находили по формуле:

                                         G_ж = (V_вх,в - V_вых,в)×М/22,4                                       (2.39)

          Таким образом, в разделах 2.4.1. и 2.4.2. приведен математический аппарат, формализующий химические превращения веществ и изменение их агрегатных состояний. Перейдем теперь к вопросу формализации процессов обмена тепловой энергией.

          2.4.3. Процессы теплообмена.

2.4.3.1. Основные положения и принятые допущения.