Методические основы построения математической модели совместного производства, страница 7

          При движении газа (жидкости) в межтрубном пространстве кожухотрубчатого теплообменника с сегментными перегородками критерий Нуссельта определяли следующим образом [48]:

 при  Re ³ 1000: 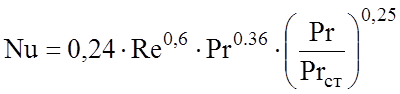                                       (2.52)

 при  Re < 1000: 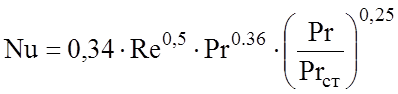                                      (2.53)

В [33] утверждается, что при развитом пузырьковом кипении интенсивность тепловыделения растет при увеличении плотности теплового потока и давления и практически не зависит от размеров и формы теплоотдающей поверхности. Эта зависимость характерна для любых жидкостей, смачивающих поверхность нагрева. Для чистой воды коэффициент теплоотдачи при кипении определяли по формуле [77]:

                                                   a_в = 3,14×q^0.7×P_нп^0,15                                        (2.54)

где Р_нп – давление насыщенных паров воды, ати; q – удельная тепловая нагрузка, Вт/м².

В рассматриваемом нами процессе конденсация происходит в присутствии неконденсируе­мых компонентов, т.е. при неизотермических условиях. Согласно [76] при концентра­ции неконденсируе­мых компонентов с_неконд > 80 % используется коэффициент теплоотдачи, рассчитанный для газовой смеси. Данное условие выполняется при конденсации метанола-сырца (с_неконд » 95 %). При конденсации воды с_неконд » 60-70 %, но в рассмотренной нами литературе нет надежных данных для определения a в таких случаях, поэтому мы и здесь вычисляли a как для газовой смеси.

По рекомендациям [76] в приближенных расчетах коэффициенты теплоотдачи мы вычисляли при средних температурах теплоносителей.

2.4.3.3. Определение средней разности температур

             и поверхности теплопередачи.

          В аппаратах с противоточным движением тепло­носителей Dt_ср при прочих равных условиях больше, чем в случае прямотока, поэтому все теплообменники будем рассчитывать как противоточные. В этом случае среднюю разность температур потоков вычисляли как среднелогарифмическую между большей и меньшей разностями температур теплоносителей на концах аппарата [48]:

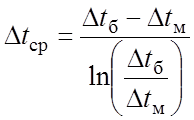                                                                                                (2.55)

          После определения Q, K и Dt_ср из уравнения (2.40) определяется  необходимую поверхность теплообмена F. Поскольку мы проводили поверочные расчеты, то выбранный заранее теплообменник обладает фактической поверхностью теплообмена F_ф. Таким образом, возникает некоторый запас поверхности:

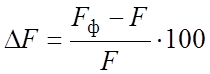                                                                                              (2.56)

          Если DF < 0, то выбирали другой теплообменник и повторяли расчет. Нормальным считается запас поверхности 5­­­-10 % [48].

          Итак, мы рассмотрели основной математический аппарат для расчета процессов теплообмена, проводимых в стандартном оборудовании.

         2.4.4. Утилизация тепла синтеза метанола.

          Как было показано в разделе 1.4, набольшее значение при организации теплообмена в производстве метанола имеет вопрос утилизации тепла реакций синтеза. В разделе 2.2 автор диссертации указывал, что процесс синтеза метанола необходимо рассматривать на уровне области аппарата. В реакторе такой областью является слой катализатора в трубке.

В ходе моделирования мы предположили, что процесс в реакторе протекает в режиме идеального вытеснения. Практически это означает, что радиальными градиентами температур и концентраций в слое, а также продольной теплопроводностью и диффузией можно пренебречь [19]. Далее дана оценка корректности такого допущения.

Как известно [20], возникновение радиального градиента температуры зависит от условий теплоотвода, определяемых критерием Био Bi, и интенсивности тепловыделения, зависящей от разности температур между слоем катализатора и ''холодильником'' q_ср- q_х (здесь q - безразмерные температуры). Согласно [20] профиль температуры по радиусу будет близок к плоскому, если:

Bi×( q_ср- q_х) < 1

          Там же [20] указывается, что для синтеза метанола комплекс Bi×( q_ср- q_х) равен приблизительно 0,07. Плоский профиль температуры означает равенство скоростей реакций в радиальном направлении. Следовательно, радиальными градиентами концентраций также можно пренебречь.

          Многочисленные расчеты, проведенные в широком интервале изменения всех параметров, показали, что если критерий Пекле Ре > 200, то продольный перенос можно не учитывать [20]. Расчет по модели идеального вытеснения в рассматриваемом нами процессе дает следующие значения: Ре = 1780-1940 (Ре изменяется по высоте трубы).

          Таким образом, показано, что применение модели идеального вытеснения не приведет к существенным ошибкам.

 Нами рассматривался процесс в одной трубке сечением S, через которое проходит газовая смесь. Затем мы предположили, что процесс протекает во всех трубках реактора одинаково. Координата по направлению потока – длина трубки l. По мере прохождения потока реакционной смеси вследствие химических превращений изменяются концентрации компонентов и температура потока. Одновременно происходит теплообмен через стенку с кипящей в межтрубном пространстве водой.  Конвективный теплообмен описывали законом Ньютона-Рихмана [24,33]:

dQ = a×dF ×(T_г – Т_ст),

а теплообмен путем теплопроводности – законом  Фурье [24,33]:

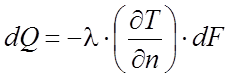
Исходя из вышеописанных положений, для элементарного объема – слоя высотой dl и объемом dv = S×dl - процесс описали следующей системой уравнений:

                              dn₁ = r₁×dv                                                                            (2.57)

                              dn₂ = r₂×dv                                                                            (2.58)

                              N×c_p×dT = (Q₁× dn₁ –  Q₂× dn₂) - a_г×dF_ст,вн×(T_г – Т_ст,вн)             (2.59)