Методические основы построения математической модели совместного производства, страница 2

2) описание различных процессов (физические, химические, механические и др.), протекающих на различных стадиях ХТЭС, также с помощью математических уравнений;

3) расчет для каждой подсистемы материального и теплового балансов, т.е. обеспечение соблюдения законов сохранения на каждой стадии производства;

4) проведение поверочного расчета для нового оборудования исходя из определенных на уровне 3 нагрузок на аппараты;

5) объединение отдельных подсистем в систему, при этом между ними возникает большое число связей, обусловленных движением материальных и тепловых потоков от одного аппарата к другому. Другими словами, необходимо отразить в модели обмен веществом и энергией между стадиями производства, основываясь на законах сохранения;

6) вывод общих параметров ХТЭС и расчет экономических показателей.

Каждый следующий уровень описания ХТЭС наследует существенные свойства предыдущего уровня.

          На рис. 9 приведена соответствующая структурная схема, отражающая построение модели ХТЭС как бы ''по вертикали''.

          Построение модели ''по горизонтали'' отражено на рис. 10, где указаны основные расчетные блоки модели и связи между ними.

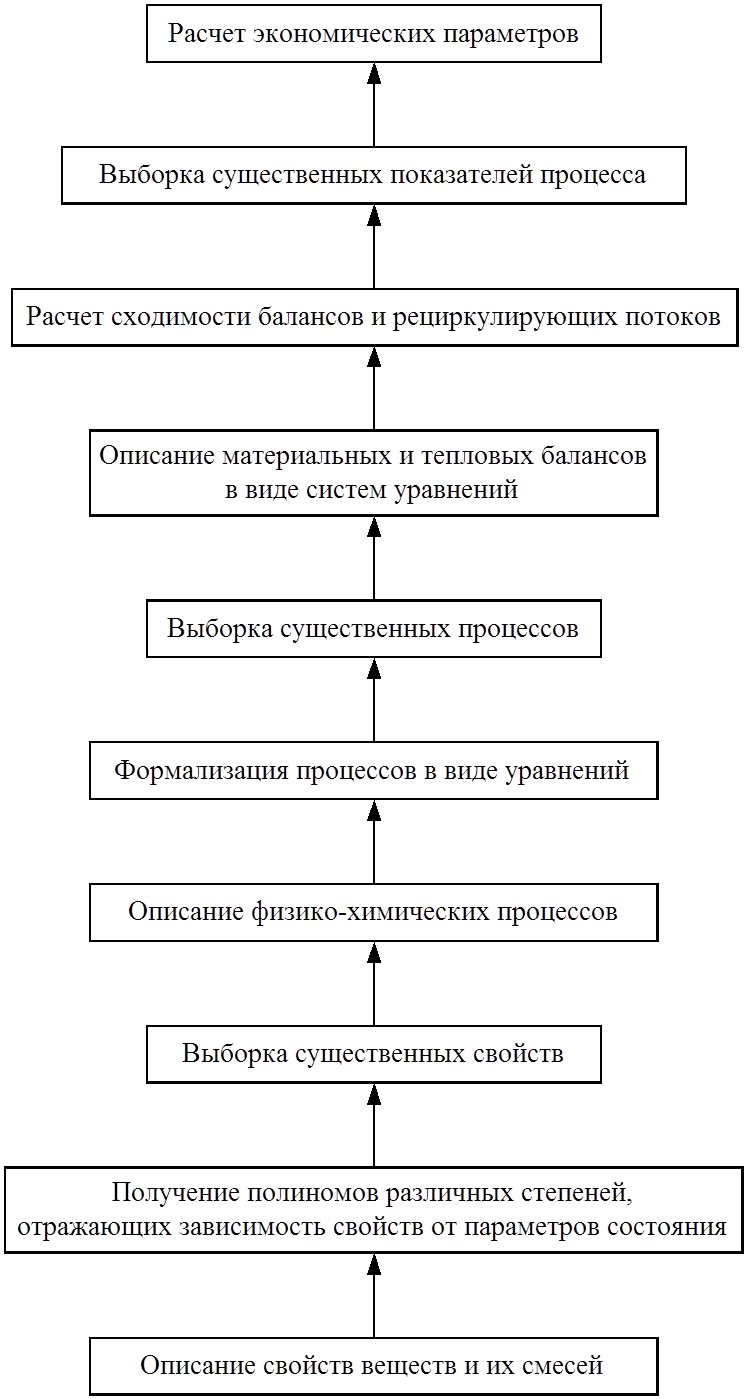
Рис. 9. Структурная схема построения модели ХТЭС ''по вертикали''.

          На рис. 10 приняты следующие условные обозначения: V – объемный расход, G – массовый расход, N_i – состав потока, t – температура, Р – давление, N – мощность. В штриховых прямоугольниках указаны параметры, которые должны быть заданы, остальные параметры являются расчетными.

          Данная структурная схема является ''ядром'' модели, на ней указаны лишь основные расчетные блоки и связи между ними. Далее будет показано, что необходимо провести еще ряд поверочных расчетов с целью определения существенности влияния того или иного физико-химического процесса (например, растворение газов), расчеты аппаратов на прочность и др.

          На схеме также указаны точки ''разрыва'' замкнутых рециркулирующих потоков. Это сделано для того, чтобы система стала разомкнутой. Более подробно данный вопрос обсуждается в разделе 2.6.

          Следующие разделы данной Главы посвящены формализации объекта исследования. В них приведен математический аппарат, описывающий каждую подсистему согласно принятой структуре. Кроме того, критически оцениваются все принятые допущения и на каждом уровне описания определяются существенные свойства ХТЭС.

2.3. Моделирование свойств веществ и их смесей.

          Для моделирования физико-химических процессов необходимо задать свойства веществ, их зависимость от температуры и давления, а также определить правила и уравнения для вычисления свойств смесей. Приступим к описанию свойств веществ:

    1) характеристики индивидуального вещества: критические параметры (температура Т_с, давление Р_с, объем V_c, коэффициент сжимаемости Z_c), температура кипения Т_b (при давлении 1 атм), молярная масса М, фактор ацентричности Питцера w - все данные взяты из [59].

    2) теплоемкость и энтальпия

Зависимость удельной изобарной теплоемкости газа c_p (Дж/(моль×К)) от температуры T (К) описали полиномом 3-й степени с коэффициентами из [59] (начальная точка – 1 атм, 298 К):

c_p = a + bT + cT² + dT³                                    (2.1)

          Зависимость знтальпии газа от температуры можно найти, проинтегрировав уравнение Кирхгофа [30]:

                                                  

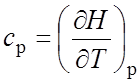
Выражение (2.1) интегрировали в пределах от 298 до t+273:

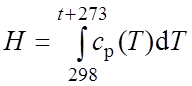                                               (2.2)

          Таким образом получали зависимость удельной энтальпии (Дж/моль) от температуры (°С) в виде полинома четвертой степени для каждого компонента газовой смеси:

                                                   Н = f(t)                                                               (2.3)

          Тот факт, что энтальпия (теплоемкость) газа зависит от давления, можно математически выразить следующим образом:

                                                   Н = f(t) + Н'(P,t)                                           

где Н'(P,t) – поправка на давление, зависящая как собственно от давления, так и от температуры. Причем при Р = const Н' слабо зависит от температуры. Например, при расчете по методу Ли-Кеслера [59] для метанола при Р = 10 атм и t = 240…300 °С Н' = -828…-615 Дж/моль, что составляет не более 3% от величины Н. На всех рассматриваемых нами стадиях ХТЭС давление изменяется незначительно (не более 2 атм), т.е. можно полагать Р » const и Н ' » const. Тогда все поправки на давление, входящие в левую и правую части уравнения теплового баланса, взаимно сократятся. Таким образом, можно не учитывать влияние давления на энтальпию (теплоемкость) газов, что не приведет к большим погрешностям.

          Зависимость удельной энтальпии Н (кДж/кг) перегретого водяного пара от температуры t (°С) и давления Р (атм),  удельной энтальпии  насыщенного водяного пара и водяного конденсата от температуры получили аппроксимацией табличных данных из [57]:

                                                   Н_п.п. = f(Р,t)                                                       (2.4)

                                                   Н_н.п. = f(t)                                                          (2.5)

                                                   Н_в.к. = f(t)                                                           (2.6)

          Также аппроксимацией табличных данных из [82] получили зависимость теплоты конденсации метанола от температуры:

                                                   Н_конд.м. = f(t)                                                                (2.7)

          Уравнения (2.4-2.6) являются полиномами различных степеней.