Методические основы построения математической модели совместного производства, страница 4

5) синтез аммиака

                                         N₂ + 3Н₂  « 2NH₃, DН < 0                                       (2.21)

6) синтез метанола описывается двумя независимыми реакциями. В [39,82,87] рассматривают реакции:

СО + 2Н₂ « СН₃ОН, DН = - 90,73 кДж                          (2.22)

                              СО₂ + Н₂ « СО + Н₂О, DН = 41,2 кДж                            (2.23)

Розовский А.Я. и др. показывают [21,29,45,61-64,89], что более правильно рассматривать реакции:

СО₂ + 3Н₂ « СН₃ОН + Н₂О                                              (2.24)

                              СО + Н₂О « СО₂ + Н₂                                                      (2.25)

Предлагаемые кинетические уравнения для этих  реакций довольно сложны. В программе, описанной в [35],  кинетика синтеза метанола может быть рассчитана на основе реакций (2.22,2.23) или реакций (2.24,2.25), а также и по третьему варианту на основе так называемого механизма смешанного типа. В [87] предлагается довольно простое кинетическое уравнение реакции (2.37) на медьсодержащем катализаторе, поэтому в математической модели мы решили рассматривать реакции (2.22,2.23). При наличии  достаточных данных разработанная модель легко адаптируется к реакциям (2.24,2.25).

При синтезе метанола протекают также побочные реакции. В рассмотренной литературе [21,29,44,46,61-64,88] нет данных о кинетике побочных реакций, а по практическим данным [13] общее содержание побочных продуктов не превышает 0,2 % мол. Поэтому в модели мы пренебрегли побочными реакциями.

7) реакции горения природного газа (т.е. метана и его гомологов):

C_nH_2n+2 + (3n+1)/2O₂ = nCO₂ + (n+1)H₂O, DН < 0                       (2.26)

Мы полагаем, что для балансовых расчетов допустимо принять следующее:

-  реакции горения протекают до конца;

-  реакции окисления азота отсутствуют.

Материальный баланс реакций горения вычисляется покомпонентным сложением и вычитанием согласно стехиометрии реакций (2.26) с учетом принятого коэффициента избытка воздуха.

Тепловые эффекты реакций (2.26) известны из литературы [74].

Равновесие реакций (2.13, 2.14, 2.21) выражается через константу равновесия:

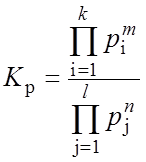,                                                   (2.27)

где р_i – парциальные давления продуктов реакции; p_j – парциальные давления исходных веществ; m, n - стехиометрические коэффициенты. Зависимости констант равновесия от температуры известны [53,66,74]. Парциальное давление компонента газовой смеси определяли по закону Дальтона:

p_i = N_i×Р                                                    (2.28)

где N_i – мольная доля компонента в равновесной газовой смеси; Р – общее давление в системе.

          Закон Дальтона справедлив, если в области температур и давлений, при которых протекает процесс, ни один из компонентов газовой смеси не находится вблизи своей критической точки или линии конденсации. Из всех стадий производства аммиака параметры вторичной конверсии СО наиболее близки к линии конденсации воды. Анализ системы с помощью пакета ChemCAD  показал, что область конденсации воды достаточно далека от области температур и давлений вторичной конверсии СО, поэтому для описания равновесия мы использовали (2.27,2.28). Кроме того, на основе этих же рассуждений приняли, что мольная доля компонента в газовой смеси выражается как:

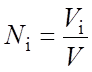                                                  (2.29)

где V_i– объем компонента в газовой смеси; V - общий объем смеси. Все объемы выражены в нм³.

          В случае, если в системе протекает несколько химических реакций, то, записав уравнение (2.27) для каждой реакции, получали систему уравнений. Методика, подобная предлагаемой нами, описана в [19].

          Для корректности расчета по формуле (2.27) необходимо применить  способ учета  недостижения равновесия реакций  Чтобы излишне не усложнять модель, мы использовали метод приближения к равновесию по температуре [23]:

DT = Т_р  -  Т_ф                                                  (2.30)

где Т_ф – фактическая температура на выходе; Т_р – равновесная температура (равновесное содержание целевого продукта реакции после реактора равнялось бы фактическому). Для экзотермических реакций DТ > 0, для эндотермических DТ < 0.

          Метод позволяет формально оценить такие параметры, как неравномерное распределение газа по сечению катализатора, уменьшение каталитической активности катализатора и т.д. Конечно, метод имеет принципиальный недостаток: при изменении режима работы реактора меняется само значение DТ.  Тем не менее, мы посчитали данный метод пригодным для балансовых расчетов.

Уравнения для расчета констант равновесия реакций (2.13, 2.14, 2.21, 2.22, 2.23) и скоростей реакций (2.22,2.23) взяты из [66,74,82,87] и приведены в Приложении III.

2.4.2. Процессы конденсации.

В синтезе аммиака (см. рис. 7) присутствуют стадии аммиака, для их математического описания наиболее пригодны уравнения Михельса [66,74], приведенные в Приложении III (формулы 15-18).

          В контуре метанола (см. рис. 8) присутствует стадия конденсации из газовой смеси метанола и воды. Для балансовых расчетов было принято [19], что при конденсации жидкая и газовая фаза находятся в равновесии. Тогда для каждого конденсирующегося компонента смеси справедливо следующее уравнение [59]:

y_i×F_i×P = g_i×x_i×P_нас,i×F_s,i×П_i                                          (2.31)

где y - мольная доля компонента в газовой фазе, рассчитанная для нормальных условий; F - коэффициент фугитивности компонента в газовой смеси; Р – общее давление в системе; g - коэффициент активности компонента в жидкой фазе; x – мольная доля компонента в жидкой фазе; Р_нас – давление насыщенных паров компонента при заданной температуре без учета влияния давления; F_s - коэффициент фугитивности жидкости;  П – поправка Пойнтинга, учитывающая влияние давления на объем сконденсировавшейся жидкости.