Физико-химические свойства природных газов. Пересчет состава газа и конденсата, страница 5

Трехпараметрические уравнения состояния.

Дальнейшее уточнение уравнений состояния вида  Ван-дер-Ваальса проведены Пенгом и Робинсоном, которые учли еще один параметр – фактор ацентричности, введенный Питцером. Он учитывает силы, связанные с несферичностью молекул, чем форма молекулы ближе к шару, Тем меньше значение фактора ацентричности. Численное значение для каждого компонента определяется по формуле:

ω= –lg∙Р_пр–1,00                                                                                 (2.4.10)

где ω – фактор ацентричности; Р_пр=РV/Р_с – приведенное давление; РV – давление насыщенных паров при приведенной температуре Т_пр=Т/Т_с.

Для комплексного компонента С₅₊, С₆₊  значение фактора ацентричности определяют по формуле:

                                                                        (2.4.11)

Для смеси газов значение равно:

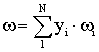                                                                                      (2.4.12)

Критические параметры С₅₊, С₆₊  находят используя значения молекулярной массы М_С5+, М_С6+ и плотности углеводородной жидкости ρ_С5+, ρ_С6+ по формулам (2.3.4) и (2.3.5).

Значение Т_крi/Т_кип можно найти по корреляционной зависимости Г.Р. Гуревича:

Т_кр.i/Т_кип=2,1898–0,1735(Т_кр.i/100)=0,006854(Т_кр.i/100)²                     (2.4.13)

при 540≤Т_кр.i≤775К           372≤Т_кип≤625К

Уравнение Пенга-Робинсона позволяет с приемлемой точностью определить объем, состав, плотность жидкой фазы, калорические и термодинамические свойства смесей при высоких давлениях и температурах. Уравнение Пенга-Робинсона относительно коэффициента сверхсжимаемости Z имеет вид:

Z³–Z²∙(1–b)+Z∙(а–3b²–2b)–(аb–b²–b³)=0                                            (2.4.14)

где                                                                                      (2.4.15)

                                                                                             (2.4.16)

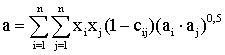                                                             (2.4.17)

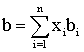                                                                                         (2.4.18)

                                                                         (2.4.19)

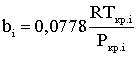                                                                              (2.4.20)

                                                                      (2.4.21)

                                           (2.4.22)

где С_ij – поправочный коэффициент парного взаимодействия.

С использованием третьего параметра для инженерных расчетов используют графический способ определения коэффициента сверхсжимаемости, который определяют по двум графикам, т.е.

Z=Z₀(Р_пр,Т_пр)+Z₁(Р_пр,Т_пр )ω                                                                (2.4.23)

Значение Z₀ и Z₁ находят по соответствующим графикам, приведенным на рисунках 2.4.5 и 2.4.6.

 

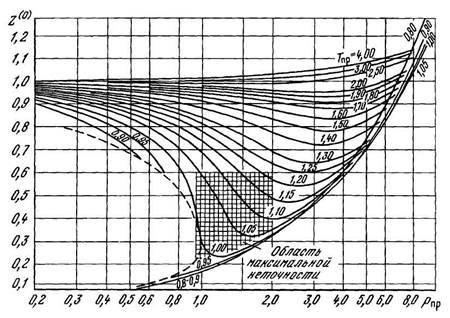
Рисунок 2.4.5 – Зависимость коэффициента сверхсжимаемости Z⁽⁰⁾простых веществ от приведенных давления и температуры.

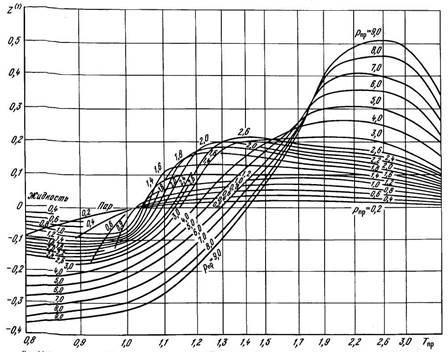
Рисунок 2.4.6 – Зависимость коэффициента сверхсжимаемости Z⁽¹⁾ несферических молекул от приведенного давления и температуры.

Для оценочных расчетов пользуются аппроксимацией графиков Брауна и Катца, предложенных Г. Гуревичем и В. Латоновым в виде:

                                                        (2.4.24)

При наличии неуглеводородных компонентов в составе природного газа N₂ , СО₂ , Н₂S более 5% каждого коэффициент сверхсжимаемости определяют по принципу аддитивности:

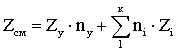                                                                      (2.4.25)

где Z_см , Z_y – коэффициенты сверхсжимаемости смеси и углеводородов; n_y – мольная доля углеводородов в смеси; к – число неуглеводородных компонентов; n_i – мольная доля i-го неуглеводородного компонента; Z_i –  коэффициент сверхсжимаемости i-го неуглеводородного компонента, определяются по графикам для каждого компонента (см. рисунок 2.4.2÷2.4.4).

2.5. Расчет плотности, физических и теплофизических свойств природного газа и конденсата.