Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов

ГЛАВА ВТОРАЯ. Идентификация статических нелинейных элементов

Введение

К статическим элементам (объектам) обычно относят элементы, параметры которых могут быть однозначно определены в статике или при изменяющихся сигналах. Особеностью этого класса объектов является то, что форма их отклика на некоторое тестовое воздействие не изменяется при варьировании масштаба времени входного сигнала. Для этих объектов можно сжимать или растягивать по времени входной сигнал, при этом выходной сигнал будет так же изменять свой масштаб, сохраняя в новой системе отсчета времени свою форму. Статические объекты принципиально не могут иметь переходных процессов (смотри рисунок 1.1), и, соответственно, они обладают нулевой динамической памятью.

Нелинейные статические объекты у(х) отличаются от линейных тем, что для них не соблюдается принцип суперпозиции:

y(x₁+x₂)¹ y(x₁)+y(x₂). (2.1)

2.1. Описание статического нелинейного элемента степенным рядом

Статические нелинейные элементы у(х) можно описывать различными способами. Одним из наиболее распространенных способов их описания является использование степенного ряда:

На практике требуется описать исследуемую нелинейность с некоторой наперед заданной точностью внутри заданного интервала изменения входной величины от min(х) до maх(х). Обычно это удается сделать, приближая исследуемую нелинейность у(х) конечным отрезком степенного ряда:

При этом задача идентификации сводится к определению последовательности из (n+1) коэффициентов. Эта задача, например, может быть решена через формирование системы линейных уравнений и определения входящих в нее неизвестных. Система, построенная для (n+1) узловых точек аппроксимации, в которых значения функции у(х) совпадает со значениями приближающего полинома, выглядит следующим образом:

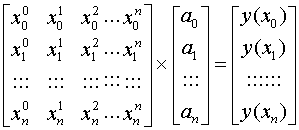(2.4)

Решение системы обычно осуществляется на компьютере путем использования одной из множества стандартных программ.

2.1.1. Погрешность приближения

В промежутках между узлами аппроксимации x₀, x₁,…, x_n значения приближающего полинома (2.3) не совпадают с исследуемой функцией у(х), причем обычно при переходе через узловую точку аппроксимации знак погрешности приближения изменяется. Пример приближения некоторой функции полиномом второй степени и график погрешности приближения приведены на рисунке 2.1.

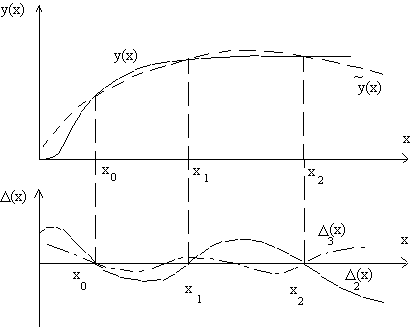
Рис. 2.1. Пример аппроксимации полиномом и

графики погрешностей приближения

Погрешность приближения можно уменьшить, увеличивая число узлов аппроксимации, что эквивалентно повышению степени аппроксимирующего полинома. На рисунке 2.1. пунктиром приведен график погрешности приближения полиномом третьей степени. Из рисунка видно, что погрешность полинома третьей степени внутри интервала приближения существенно меньше, чем погрешность приближения полиномом второй степени.

Следует отметить, что это уменьшение погрешности обусловлено не только повышением степени приближающего полинома. Важную роль играет расположение узлов аппроксимации. Погрешность приближения уменьшается, если узлы аппроксимации располагаются реже в центре интервала приближения и чаще по мере приближения их к краям интервала аппроксимации.

Оптимальное расположение узлов аппроксимации приближающего полинома степени (n) совпадает с расположением корней полинома Чебышева степени (n) при условии совпадения минимального и максимального значений корней с крайними точками интервала приближения.

Погрешность приближения полиномом степени (n):

грубо может быть оценена с помощью остаточного члена ряда Тейлора:

Таким образом, погрешность приближения зависит от числа используемых узлов аппроксимации и их расположения. Для (гладких) аналитических нелинейных зависимостей погрешность аппроксимации может быть сделана как угодно малой путем увеличения степени полинома приближения. При этом по мере повышения точности приближения и роста степени приближающего полинома приходится сталкиваться с проблемой решения систем линейных уравнений большой размерности.

2.1.2. Проблемы решения систем линейных

уравнений большой размерности