Описанные выше статические процедуры идентификации на практике не всегда просто реализуемы. Могут возникнуть ситуации, когда не удается долго поддерживать заданное значение входной постоянной величины, соответствующей выбранному узлу аппроксимации. Более того, на практике очень часто оказывается вообще невозможно подать на вход исследуемой нелинейности постоянное тестовое воздействие, так как предшествующие элементы не пропускают постоянную составляющую. В этой ситуации приходится использовать переменное входное воздействие и вылавливать моменты перехода входного сигнала через заданное значение узла аппроксимации, что крайне неудобно.
2.1.4. Идентификация нелинейного элемента в динамике
Так как переменные тестовые воздействия на практике проще реализовать, рассмотрим особенности идентификации статического нелинейного элемента у(х) в динамике. Будем считать, что мы возбудили систему, где содержится исследуемая нелинейность и на ее входе можем наблюдать некоторое тестовое воздействие х(t). На выходе нелинейности мы наблюдаем отклик у(t). Требуется построить приближающий полином y^(t) (x), отклик которого близок отклику исследуемой нелинейности:
|
y(t)» y^(t)= |
n å ak× xk(t) k=0 |
(2.9) |
Неизвестные коэффициенты полинома приближения могут быть определены путем решения системы линейных уравнений, сформированной для отсчетов, полученных в различные моменты времени:
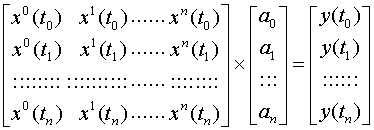(2.10)
Для того, чтобы система (2.10) содержала линейно независимые уравнения, требуется выбирать такие моменты времени, в которые сигнал х(t) принимает различные значения. Для улучшения обусловленности системы желательно, чтобы значения отсчетов x0(t), x1(t), …, xn(t) образовывали сетку, приблизительно равномерно покрывающую интересующий нас диапазон изменения входных сигналов.
Очевидно, что при попытках решить систему (2.10) могут возникнуть проблемы, связанные с ее плохой обусловленностью. Ослабить эти проблемы удается за счет повышения усреднением точности исходных данных.
В динамике усреднение обычно осуществляют по интервалу наблюдения:
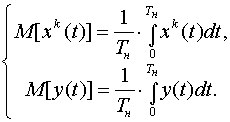(2.11)
При такой процедуре усреднения систему линейных уравнений приходится формировать на различных реализациях тестовых воздействий x0(t), x1(t), …, xn(t). Для того, чтобы получить систему линейно независимых уравнений, необходимо использовать реализации входных воздействий, отличающиеся между собой амплитудой, формой или плотностями распределения значений :
p(xi)¹ p(xk),
M[xi] ¹ M[xk].
Только при соблюдении этих условий система вида:
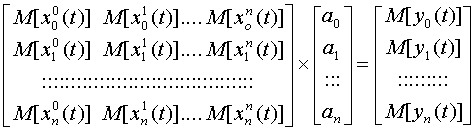(2.12)
будет содержать линейно независимые уравнения и может быть решена.
Усредняющие динамические алгоритмы идентификации не дают возможности точно указать расположение узлов аппроксимации приближающего полинома. Усредненная относительная погрешность приближения для этого класса алгоритмов оценивается следующим образом:
(2.13), где 
- отклик модели.
2.1.5. Снижение вдвое размерности решаемой системы линейных уравнений
Рассмотренные выше усредняющие алгоритмы идентификации позволяют не только поднять точность исходных данных, но и в ряде случаев многократно улучшить обусловленность решаемой задачи за счет снижения размерности решаемых систем линейных уравнений. Причем улучшение обусловленности и снижение размерности решаемых систем происходит без снижения степени приближающего полинома и, соответственно, без ухудшения точности аппроксимации.
Все это становится возможным при специальном подборе тестовых воздействий, позволяющем независимо находить четные и нечетные коэффициенты приближающего полинома. Дело в том, что тестовые воздействия с симметричной плотностью распределения значений:
р(х) = р(-х). (2.14)
имеют нулевое математическое ожидание для нечетных степенных функций:
M[x2k-1(t)]=0. (2.15).
Это позволяет определять четные коэффициенты полинома приближения независимо, решая следующую систему:
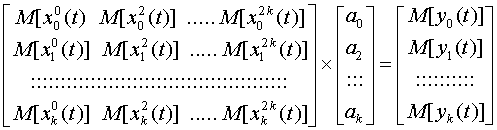(2.16)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.