Для описания исследуемой нелинейной зависимости может использоваться множество вариантов ортогональных функций. Возникает задача выбора системы наиболее выгодных базисных функций. Эта задача была решена Сверкуновым в работе [11], где он показал, что оптимальной будет являться система ортогональных базисных функций, для которой интервал ортогональности совпадает с динамическим диапазоном изменения входного сигнала, а весовая функция совпадает с плотностью распределения значений входного сигнала:
p(x) = s(x). (2.47)
При выполнении этого условия дробь s(х)/р(х)=1, что приводит к существенному упрощению формулы вычисления коэффициентов ортогонального ряда. Эта формула приобретает следующий вид:
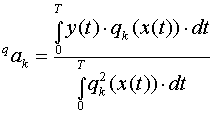(2.48) , где Т - период входного воздействия
для периодических сигналов или период наблюдения для случайных тестовых
сигналов.
Исходя из критерия оптимальности Сверкунова (2.47), можно утверждать, что для случайных и детерминированных тестовых воздействий с равномерной плотностью распределения значений: р(х)=с (2.49) оптимальными будут являться полиномы Лежандра Рk(х), весовая функция которых постоянна.Для этих полиномов и входного сигнала с равномерной плотностью распределения значений условие Сверкунова (2.47) выполняется с точностью до некоторого мультипликативного множителя b. Можно показать, что появление множителя b в условии (2.47) не приводит к нежелательным результатам. То есть, условие оптимальности Сверкунова может быть обобщено следующим образом:
p(x)=b s(x). (2.47а).
Необходимость в масштабирующем коэффициенте b обусловлена тем, что весовая функция при ортогональных полиномах формально может быть любого масштаба, а плотность распределения значений входного сигнала - это вполне конкретная физическая характеристика с единичным интегралом по динамическому диапазону входной величины.
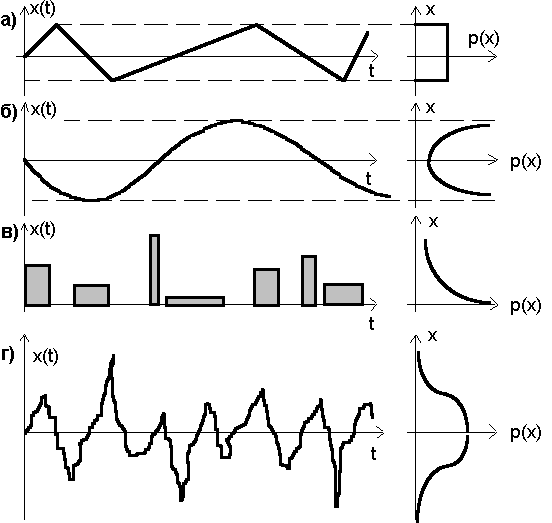
Рис. 2.3. Оптимальные тестовые воздействия и их плотности распределения значений для а) - полиномов Лежандра, б) - полиномов Чебышева, в) - полиномов Лагерра, г) - полиномов Эрмита
В частности для полиномов Лежендра с интервалом ортогональности от -1 до +1 и s(x)=1 плотность распределения входного оптимального сигнала составляет p(x)=0.5. Соответственно, соотношение оптимальности Сверкунова (2.47) не выполняется без введения b =0.5.
Для случайных и детерминированных сигналов с плотностью распределения значений синусоидального сигнала:
p(x) = 1/(1-x2)1/2 (2.50)
оптимальными будут являться полиномы Чебышева Тк(х).
Для тестовых сигналов с экспоненциальной плотностью распределения значений:
p(x) = l × exp(-l × x). (2.51)
оптимальными являются ортогональные полиномы Лагерра Lk(х). Параметр распределения l фактически является масштабным коэффициентом линейного преобразования исходной системы координат, в которой классические полиномы Лагерра становятся оптимальными для конкретного тестового воздействия.
Для случайных и детерминированных сигналов с нормальной плотностью распределения значений:
p(x) = {(2p )-1/2/s }exp(-(x/s )2/2) (2.52)
оптимальным будет являться использование системы ортогональных полиномов Эрмита. Оптимальным будет ряд Эрмита в системе координат, полученной заменой: x^ = 2-1/2× x/s .
Примеры оптимальных детерминированных сигналов и графики их плотностей распределения значений приведены на рисунке 2.3. Примеры случайных тестовых сигналов с соответсвующими плотностями распределения приводить на рисунке безсмысленно, так как разница между подобными сигналами трудноуловима при зрительном восприятии.
В заключении следует еще раз подчеркнуть, что для любого тестового воздействия (детерминированного или случайного) существует вполне определенная система оптимальных ортогональных функций. При использовании только этой системы базисных функций происходит существенное упрощение процедур идентификации статических нелинейных элементов.
2.2.6. Трансформация произвольного ортогонального
базиса к системе оптимальных базисных функций
Предположим, что динамический диапазон изменения входного сигнала х(t) точно совпадает с интервалом ортогональности выбранной системы базисных функций. Если это условие не выполняется, то добиться выполнения его можно путем линейного преобразования исходной системы координат, как это осуществлялось в параграфе 2.2.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.