Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов, страница 7

Появление в формуле (2.44) модуля производной входного воздействия обусловлено тем, что при переходе с монотонно возрастающего участка на монотонно падающий участок х(t) происходит смена знака производной и смена местами пределов интегрирования статического интеграла (2.19). Наложение двух этих эффектов и учитывается введением модуля производных в подынтегральные произведения (2.44).

Таким образом, мы получили возможность определять параметры ортогонального ряда в динамике при простейших периодических тестовых воздействиях с двумя монотонными участками, приходящимися на период. Далее будут рассмотрены более сложные тестовые сигналы.

2.2.4. Идентификация коэффициентов ортогонального ряда

при тестовых воздействиях общего вида

Усложним задачу и будем рассматривать периодические тестовые воздействия с немонотонными участками подъема. Пример такого участка подъема приведен на рисунке 2.2.

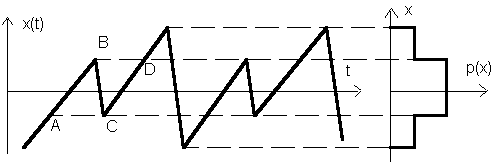
Рис. 2.2. Пример фрагмента тестового сигнала с немонотонным участком подъема и соответствующая ему плотность распределения значений р(х)

Из рисунка видно, что по немонотонному участку сигнала АВСD может произойти трехкратный учет интересующей нас информации, если мы воспользуемся для вычислений формулой (2.44). То, что сигнал х(t) на немонотонном участке несколько раз проходит одно и то же значение, учитывается его функцией плотности распределения значений р(х). В этом месте функция плотности распределения значений имеет соответствующее увеличение. По своему физическому смыслу (подробнее смотри формулу 1.40 параграфа 1.3.1.) плотность распределения значений р(х) обратно пропорциональна модулю производной в точке (х):

и прямо пропорциональна числу прохождений (i) сигнала через точку (х). Исходя из этого, мы можем заменить модуль производной входного сигнала в выражении (2.44) на обратную величину плотности распределения значений р(х). В результате получим:

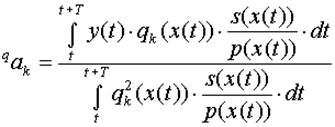(2.46)

Формула (2.46) выгодна тем, что может использоваться для любых периодических тестовых сигналов. Она автоматически учитывает многократное прохождение значений сигналов на немонотонных участках. Увеличение числа прохождений одной и той же точки, с одной стороны, увеличивает значение интегралов, а, с другой стороны, это значение пропорционально уменьшается за счет деления на увеличившееся значение плотности р(х) в точке многократного прохождения. В результате эффекты немонотонности не сказываются на значении вычисляемых коэффициентов ортогонального ряда.

Важным преимуществом формулы (2.46) является также то, что она может быть использована и для апериодических или случайных сигналов. Для ее модификации под них достаточно заменить период сигнала Т на соответствующий период наблюдения Тн за случайными сигналами. Естественно, что период наблюдения Тн для идентификации на случайных тестовых сигналах должен выбираться достаточно большим.

Следует отметить, что для случайных тестовых сигналов типа "белый шум" определить корректно процедуру дифференцирования трудно. В этом плане формулы, содержащие производную входного воздействия, становятся некорректными. Процедура же определения плотности распределения значений корректна для любой реализации случайного сигнала в случае выбора достаточного интервала наблюдения. Для сравнительно коротких интервалов наблюдения может быть вычислена оценка плотности распределения значений.

Таким образом, формулы типа (2.44) следует использовать при определении коэффициентов ортогонального ряда только на детерминированных хорошо дифференцируемых тестовых сигналах. Во всех остальных случаях следует использовать формулы типа (2.46), однако при этом оценка коэффициентов ряда в реальном времени становится невозможной. Сначала приходится вычислять плотность распределения значений используемой реализации тестового сигнала и только после этого можно приступить к вычислению коэффициентов полинома приближения.

2.2.5. Оптимальные ортогональные функции