Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов, страница 5

(2.22)

осуществляется путем следующих вычислений:

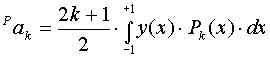(2.23)

2.2.1.2. Ортогональные полиномы Чебышева

Полиномы Чебышева T_k(x)=cos(k× arccos(x)) (2.24) ортогональны с весом:

s(x) = 1/(1-x²)^1/2 (2.25)

на интервале [+1,-1]. Соответственно

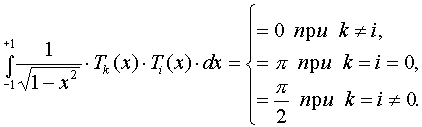(2.26).

Первые несколько полиномов Чебышева приведены в таблице 2.

Таблица 2.

Полиномы Чебышева, выраженные через степенные функции _____________________________________________________________

T₀(x) = x⁰ =1,

T₁(x)=x¹,

T₂(x) = 2x²-1,

T₃(x) = 4x³ – 3x¹,

T₃(x) = 8x⁴ – 8x²+1,

T₅(x) = 16x⁵ – 20x³ + 5x¹,

T₆(x) = 32x⁶ – 48x⁴ +18x² –1,

T₇(x) = 64x⁷ – 112x⁵ +56x³ – 7x¹,

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

где N=n/2 для четных n и N=(n-1)/2 для нечетных n.

Соседние полиномы Чебышева связаны следующим рекурентным соотношением:

T_k+1(x)=2xT_k(x)-T_k-1(x) (2.27).

Определение коэффициентов ряда Чебышева:

(2.28)

осуществляется путем следующих вычислений:

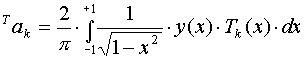(2.29).

В теории идентификации, кроме приведенных выше полиномов Чебышева первого рода T_k(x), важную роль играют полиномы Чебышева второго рода:

U_k(x)=sin(k× arccos(x)) (2.30).

Эти полиномы ортогональны между собой и ортогональны по отношению к полиномам Т_к(х). Полиномы Чебышева второго рода получаются из полиномов первого рода путем следующих преобразований:

(2.31).

Подобно ряду Фурье приближаемая нелинейность у(х) может быть описана полным рядом Чебышева, содержащим полиномы первого и второго рода:

(2.32).

Коэффициенты Tak полного ряда Чебышева (2.32) находятся соотношением (2.29), коэффициенты Uak вычисляются следующим образом:

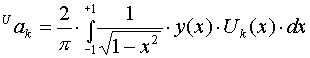(2.33).

Полиномы Чебышева второго рода не выражаются через конечные рациональные степенные полиномы.

2.2.1.3. Ортогональные полиномы Лагерра

Полиномы Лагерра L_k(x) ортогональны с весом

s(x) = exp(-x) (2.34)

на интервале [0, ¥ ]:

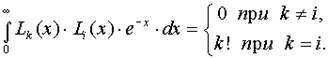(2.35).

Первые несколько полиномов Лагерра приведены в таблице 3.

Соседние полиномы Лагерра связаны следующим рекурентным соотношением:

L_k+1(x)=(2k+1-x)L_k(x)-k²L_k-1(x) (2.36).

При описании нелинейной зависимости рядом Лагерра:

(2.37)

коэффициенты этого ряда находятся по следующей формуле:

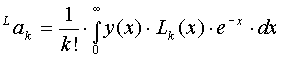(2.38).

Таблица 3.

Полиномы Лагерра, выраженные через степенные функции _____________________________________________________________

::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Необходимо отметить, что при вычислениях коэффициентов ряда Лагерра не обязательно использовать интегралы с бесконечными пределами интегрирования. На практике все вычисления призводятся с конечной точностью, что позволяет заменить бесконечные пределы интегрирования на конечные. При этом появляется некоторая погрешность вычислений, значения которой для различных пределов приведены в таблице 4.

Таблица 4.

Пределы интегрирования -------------------------	3	5	10	15	¥
	0 --------------	0 ------------	0 -----------	0 ------------	0 ------------
Ошибка вычислений	49.2%	16.96%	0.44%	0.045%	0

2.2.1.4. Ортогональные полиномы Эрмита

Полиномы Эрмита H_k(x) ортогональны с весом:

s(x) = exp(-x²), (2.39)

на интервале [+¥ , -¥ ]:

Первые несколько полиномов Эрмита приведены в таблице 5.

Таблица 5.

Полиномы Эрмита, выраженные через степенные функции

:::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

,

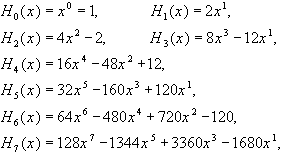
где N=n/2 для четных n и N=(n-1)/2 для нечетных n.

Соседние полиномы Эрмита связаны следующим рекуррентным соотношением:

H_k+1(x)=2x× H_k(x)-2k× H_k-1(x). (2.40).

При описании нелинейной зависимости рядом Эрмита:

, его коэффициенты находятся путем вычисления следующих интегралов:

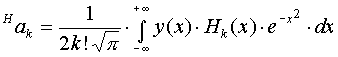
В реальных условиях осуществлять вычисление коэффициентов ряда Эрмита через интегралы с бесконечными пределами нецелесообразно. Реальные расчеты всегда проводятся с конечной точностью, что позволяет заменить бесконечные пределы интегрирования на конечные пределы. Значения ошибок, возникающих из-за подобной замены, приведены в таблице 6.