Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов, страница 6

Таблица 6.

2.2.2 Трансформация ортогональных функций к заданному

интервалу изменения входных воздействий

Формулы вычисления коэффициентов некоторого ортогонального ряда сводятся к интегрированию по интервалу ортогональности. Предположим, что мы хотим воспользоваться ортогональным рядом Лежандра, для которого интервал ортогональности [-1,+1]. Если же входное воздействие на исследуемую нелинейность изменяется в других пределах:

max(x)¹ +1,

min(x) ¹ -1, (2.41)

то необходимо осуществить линейное преобразование исходной системы координат вида х^{^} =(аx + b)с тем, чтобы неравенство (2.41) превратилось в тождество:

max(x)=+1,

min(x) =-1. (2.42).

В новой системе координат динамический диапазон изменения входного сигнала будет совпадать с интервалом ортогональности выбранного ряда Лежандра. Соответственно, мы можем для новой системы координат вычислить коэффициенты разложения исследуемой нелинейности в ряд Лежандра. После этого необходимо перейти от ортогонального полинома приближения Лежандра к обычному степенному полиному.

На заключительном этапе необходимо осуществить возврат в исходную систему координат через обратное преобразование вида х = (х^{^} - b)/а. При этом аппроксимирующий степенной полином претерпевает сравнительно простые изменения (его коэффициенты изменяются пропорционально соответствующей степени масштабного коэффициента).

Операции трансформации системы координат и перехода от ортогонального полинома к степенному полиному осуществляются подпрограммами ПЭВМ и практически не вносят дополнительных погрешностей, так как все линейные коэффициенты, участвующие в этих операциях, известны абсолютно точно (получены аналитически).

Все вышесказанное справедливо для любой системы конечных ортогональных полиномов, выражающихся через конечные степенные полиномы.

2.2.3. Определение коэффициентов ортогонального ряда в динамике на монотонных участках входного воздействия

Приведенные выше процедуры определения коэффициентов выбранного ортогонального ряда осуществлялись путем интегрирования по интервалу ортогональности по переменной х. Соответственно для их реализации мы должны линейно изменять входное воздействие от min(х) до maх(х), контролируя отклик нелинейного элемента у(х) и осуществляя интегрирование.

К сожалению, это не всегда возможно в условиях реального эксперимента. В большинстве случаев мы не можем подать на вход исследуемого нелинейного элемента линейно изменяющееся входное воздействие. Как правило, мы вынуждены довольствоваться наблюдением достаточно сложного периодического входного воздействия х(t), являющегося откликом предшествующих нелинейному элементу блоков на периодическое возбуждение системы в целом.

Предположим, что наблюдаемое входное воздействие х(t)имеет монотонно возрастающий участок, на котором сигнал изменяется от min(х) до maх(х). Воспользуемся этим участком сигнала для определения коэффициентов ортогонального ряда. Для этой цели в формуле (2.19) заменим переменную интегрирования dх на dt. В результате получим:

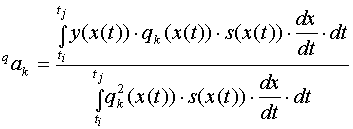(2.43), где t_i - момент времени при котором х(t) = min(х), t_j - момент времени при котором х(t) = maх(х), при всех t_i < t < t_j dx/dt > 0.

Приведенная выше формула обладает одним весьма существенным недостатком: при ее реализации необходимо точно засинхронизировать моменты начала и окончания интегрирования. На практике стараются отказаться от привязки к точкам t_j и t_i. Для этого, например, могут использоваться периодические тестовые воздействия с двумя монотонными участками подъема и спада, приходящимися на период входного сигнала. В этом случае интегрирование должно осуществляться точно по периоду входного воздействия, начиная с произвольного момента времени:

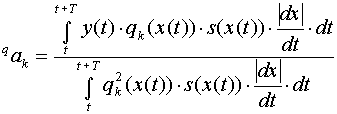(2.44)