Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов, страница 4

После решения системы (2.16) мы будем знать все четные коэффициенты полинома приближения. Зная их, можно вернуться к решению системы (2.12), где половина коэффициентов уже известна. Соответственно, эта система, сформированная на тестовых воздействиях с несимметричной плотностью распределения значений p(х) = p(-х), будет иметь вдвое меньшую размерность. Получается, что при реализации описанного выше подхода мы вместо решения полной системы из (n+1) уравнения решаем две системы из (n+1)/2 уравнений. Снижение в два раза размерности решаемых систем линейных уравнений приводит к многократному улучшению их обусловленности.

2.2. Преимущества использования ортогональных рядов

Следует отметить, что приведенное выше описание исследуемой нелинейности степенным рядом весьма удобно для интерпретации результатов, но является далеко не единственным. Для описания исследуемой нелинейной зависимости возможно использование любой другой системы базисных функций. Особый интерес представляет использование системы базисных функций, ортогональных на заданном интервале изменения входного сигнала [min(х), maх(х)]. Использование ортогонального базиса позволяет при определенных условиях вообще исключить из алгоритма идентификации плохо обусловленную процедуру решения системы линейных уравнений. Задача при этом сводится к независимому определению каждого из коэффициентов ортогонального полинома приближения.

Описание исследуемой нелинейной зависимости у(х) системой ортогональных базисных функций выглядит следующим образом:

y(x) =

¥ å qak × qk(x) k=0

(2.17)

где q_k(x) - система функций ортогональных на интервале [min(х), maх(х)] с весом s(x) и, соответственно, обладающих следующим свойством:

В силу ортогональности выбранной системы базисных функций каждый из коэффициентов ряда (2.17) может быть вычислен по следующей формуле:

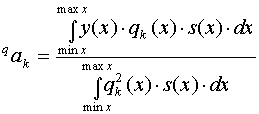(2.19)

Фактически решение системы линейных уравнений обязательное при использовании неортогонального базиса исчезает, замещаясь процедурами вычисления определенных интегралов с последующим их попарным делением. Отпадает необходимость заранее ограничивать число членов приближающего полинома, внося априорно неизвестную погрешность. Порядок использованного ортогонального полинома можно постепенно увеличивать в процессе вычислений путем учета дополнительных членов.

При этом определенные ранее коэффициенты ортогонального полинома не изменяются, а погрешность приближения полиномом сопоставима с его вновь добавленным членом.

2.2.1 Классические ортогональные полиномы

Существует бесконечное число ортогональных базисных функций. Большинство ортогональных базисных функций не выражается через конечные степенные полиномы и может быть описано только бесконечными степенными рядами. Исключением являются классические полиномы Лежандра, Чебышева, Лагерра, Эрмитта. Именно по этой причине они важны и занимают особое место среди множества возможных ортогональных функций.

2.2.1.1. Ортогональные полиномы Лежандра

Полиномы Лежандра P_k(x) ортогональны на интервале [-1,+1] с весом s(х)=1:

Первые семь полиномов Лежандра приведены в таблице 1.

Соседние полиномы Лежандра связаны следующим рекурентным соотношением:

P_k+1(x) = {(2k+1)/(k+1)}× x× P_k(x) – {k/(k+1)}× P_k-1(x). (2.21)

Таблица 1.

Ортогональные полиномы Лежандра

P₀(x) = x⁰ = 1,

P₁(x) = x¹,

P₂(x) = (1/2) (3x² – 1),

P₃(x) = (1/2) (5x³ – 3x¹),

P₄(x) = (1/8) (35x⁴ – 30x²+3),

P₅(x) = (1/8) (63x⁵ – 70x³+15x¹),

P₆(x) = (1/16) (231x⁶ – 315x⁴+105x²-5),

P₇(x) = (1/16) (429x⁷ – 693x⁵+315x³-35x¹),

::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::

Pn(x) = 2-n

N å (-1)m× m=0

(2n-2m)!× xn-2m ¾ ¾ ¾ ¾ ¾ ¾ m!(n-m)!(n-2m)!

где N=n/2 для четных n и N=(n-1)/2 для нечетных n.

Определение коэффициентов разложения нелинейности в ряд Лежандра :