Идентификация статических нелинейных элементов. Преимущества использования ортогональных рядов, страница 2

Решение системы линейных уравнений большой размерности, как правило, является плохо обусловленной задачей. Система хорошо решается только в том случае, когда исходные данные заданы с высокой точностью. Для каждой конкретной системы линейных уравнений может быть вычислено число обусловленности "соnd", которое можно рассматривать как коэффициент усиления шумов исходных данных при решении системы. Сушествует несколько способов точного вычисления числа обусловленности [7,8], наиболее просто число обусловленности оценивается следующим образом:

cond[X] @ max½ xⁱ_i,k½ /min½ xⁱ_i,i½ . (2.7)

Число обусловленности "соnd" или коэффициент усиления шумов (погрешностей) исходных данных может изменяться в пределах от 1 до ¥ . Чем больше коэффициент обусловленности, тем хуже решается система линейных уравнений. Наилучшее число обусловленности - 1 имеют системы с диагональной информационной матрицей (все элементы матрицы нулевые, кроме диагональных). По мере расползания диагональной матрицы и увеличения значений ее элементов, расположенных вне диагонали, обусловленность матрицы ухудшается. При этом ухудшение обусловленности наступает быстрее по мере увеличения значений наиболее удаленных от диагонали элементов. Любые преобразования, приводящие к стягиванию плотности распределения значений элементов матрицы к ее диагонали, приводят к улучшению обусловленности.

Число обусловленности - это очень важная характеристика алгоритма идентификации. Предположим число обусловленности соnd =100, это означает, что при погрешности измерения значений у(х) или (х) - 1% погрешность результатов, полученых после решения системы линейных уравнений, будет составлять 100%. Этим результатам вообще нельзя доверять. Для получения достоверных результатов требуется использовать специальные процедуры регуляризации решения системы [9,10] или существенно повышать точность исходных данных. В нашем случае (соnd = 100) для получения погрешности конечных результатов 1% необходимо использовать исходные данные измеренные с погрешностью 0,01%.

Число обусловленности сильно зависит от размерности решаемой системы линейных уравнений. Последнее заставляет осторожно подходить к выбору степени приближающего полинома. При попытках снизить погрешность аппроксимации за счет увеличения степени полинома приближения необходимо обязательно контролировать число обусловленности получающихся систем линейных уравнений. В каждом конкретном случае существует некоторое оптимальное значение степени полинома приближения, при котором максимальное значение погрешности аппроксимации близко к погрешности вычислений, обусловленной усилением (накоплением) погрешностей измерения исходных данных. Увеличивать степень полинома приближения по сравнению с оптимумом, имеет смысл только, если есть возможность повысить точность исходных данных за счет их предварительной статистической обработки (например усреднением).

Можно увеличить степень полинома приближения выше оптимальной за счет привлечения различных процедур регуляризации [9,10], однако этим нельзя увлекаться, так как смыслом всех процедур регуляризации является загрубление чувствительности вычислительных процедур к вариациям исходных данных. Кроме того, выбор параметров процедур регуляризации - это очень трудная задача, требующая от исследователя привлекать его интуицию и предшествующий опыт.

2.1.3. Повышение точности исходных

данных усреднением в статике

В случае, когда погрешность измерения исходных данных не содержит систематической составляющей и носит случайный характер, точность идентификации можно повысить, воспользовавшись предварительным усреднением результатов измерений. В этом случае решаемая система линейных уравнений будет выглядеть следующим образом: (2.8)

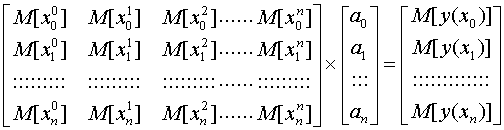
Ориентировочно можно считать нормальным закон распределения значений погрешностей измерений. Тогда усреднение N независимых измерений позволяет поднять точность исходных данных в Ö ` N раз. Соответственно, для того, чтобы поднять точность исходных данных в 10 раз, приходится увеличивать в 100 раз число независимых измерений.