Общие сведения об исследованиях и испытаниях ГПС. Общие сведения о средствах и методах измерения. Измерение частоты вращения. Емкостные преобразователи. Испытания гидро- и пневмоприводов на прочность и герметичность, страница 26

ЛЕКЦИЯ №21 31.05.13

2)Критерий Пирсона

Критерий Фишера обычно применяется для определения адекватности малых выборок. При больших выборках целесообразно применять критерии Пирсона, Романовского и Колмогорова. Критерий Пирсона широко применяется при больших статистических измерениях в соответствии с этим критерием гипотеза о законе распределения подтверждается если соблюдается условие     для нормального закона распределения 0,1. Хи – критерий согласия Пирсона q=m-s где эм – количество групп серии большой выборки эс число постоянный коэффициентов уравнений. Количество измерений или частот в каждой группе по данным эксперимента, … по данным теоретической зависимости. Уэ и уi соответственно.

Порядок определения адекватности следующий:

Пусть имеется выборка из n измерений. Статистические измерения следует разбить на m разрядов. В каждом разряде может оказаться определенное количество измерений Уэi. Строится кривая по экспериментальным данным, как правило это гипербола или парабола; Для этой эксперименатлной кривой устанавливаются теоретические частоты утi и далее вычисляется критерий Пирстона хи-квадрат по вышеприведенной формуле. Сравнивается с данными таблицы, в зависимости от числа степеней свободы и выбранным количеством разрядов или частот.

Пример: произведено N=250 измерений, по ним необходимо определить закон распределения и адекватность математической модели. Для этого экспериментальные данные yэi целесообразно разбить на m=7 групп. Результаты измерений необходимо нанести на сетку прямоугольных координат в соответствии с частотами x1 и тд x2 x3 x4 и аппроксимировать их кривой. В качестве аппроксимирующей кривой принимают кривую нормального распределения по которой соответственно устанавливают теоретические частоты.

3)Критерий Романовского

Он также работает при большой выборке N и определяется соотношением

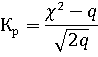
Кр=0,772<3 таким образом по критерию Пирсона и Романовского гипотеза о принаждежности экспериментальных данных к кривой нормального распределения подтверждается.

4)Критерий Колмогорова

Он также применяется для большой выборки n но в этом случае статистическую кривую частот преобразовывают в статистическую интегральную функцию находят наибольшую разность частот d₀ а это d₀ определяется  и по значениям лямбда по специальным таблицам находят вероятность .

ЛЕКЦИЯ №22

ЛЕКЦИЯ №23

ЛЕКЦИЯ №24

ЛЕКЦИЯ №25