МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ТЕОРИЯ ОБРАБОТКИ МЕТАЛЛОВ
ДАВЛЕНИЕМ
В.И. Филимонов
УДК 620.186 (076)
ББК 34.62 я 7
Т 34
Теория обработки металлов давлением: Методические указания к решению задач для студентов специальности 12.04 «Машины и процессы обработки металлов давлением»/ Составители: Ю.Н. Берлет, В.И. Филимонов. – Ульяновск: УлГТУ, 2001. - 42 с.
Сборник задач по теории обработки металлов давлением разработан в соответствии с программой курса «Теория обработки металлов давлением» и содержит основные задачи для аудиторной и самостоятельной работы студентов.
Работа подготовлена на кафедре «Материаловедения и обработки металлов давлением».
УДК 620.186 (076)
ББК 34.62 я 7
Рецензент зам. директора ФГУП «Ульяновский НИАТ»,
кандидат технических наук В.А. Марковцев
научно-методического совета университета
Учебное издание
Теория обработки металлов давлением. Методические указания к решению задач.
Составители: Берлет Юрий Николаевич, Филимонов Вячеслав Иванович
Редактор Н.А. Евдокимова
───────────────────────────────────────────────
Подписано в печать 10.01.2002. Формат 60х84 1/16. Печать трафаретная.
Бумага писчая. Усл. печ. л. 2, 40 Уч.-изд. л. 2,00
Тираж 100 экз. Заказ .
───────────────────────────────────────────────
Ульяновский государственный технический университет, 432027, Ульяновск, Сев. Венец, 32.
Типография УлГТУ, 432027, Ульяновск, Сев. Венец, 32.
Ó Оформление. УлГТУ, 2002
1. РЕКОМЕНДАЦИИ ПО РЕШЕНИЮ ЗАДАЧ В ТОМД
1.1. Алгоритм решения задач
При решении задач надлежит придерживаться указанной ниже последовательности действий:
1. Внимательно изучить условие задачи: уточнить схему и условия реализации процесса, при необходимости уточнить детали, связанные с применением материалов оснастки, условиями смазки, температурными режимами и т.д.
1. Повторить по лекционному материалу или учебнику, соответствующий раздел.
2. Выполнить эскиз к задаче, расположить соответствующим образом систему координат относительно инструмента и заготовки, нанести необходимые обозначения.
3. Выбрать метод решения задачи.
4. Сформулировать допущения.
5. Выполнить постановку задачи.
6. Решить задачу. При решении задачи следует нумеровать формулы, давать необходимые пояснения; обозначения на эскизе и в тексте задачи должны совпадать
7. Проверить расчетные формулы по анализу размерности, асимптотическому поведению.
8. Выполнить числовые расчеты. При необходимости представления распределений напряжений, деформаций рекомендуется использовать прикладную программу MathCAD версий 7.0 и выше для графического представлений решения.
10.Провести анализ решения, проверив его правдоподобность сравнением полученных значений с известными значениями соответствующих параметров, например, при вычислении напряжений можно ориентироваться на предел текучести материала; при решении уравнения Гамильтона-Кэлли значения напряжений можно проверить по значениям инвариантов и т.п..
11. Записать ответ.
1.2. Оформление контрольных заданий
Выполненые домашние контрольные задания должны удовлетворять следующим требованиям:
1. Работа выполняется в тонкой тетради с указанием на обложке «Расчетная работа по ТОМД», вариант, номер группы, фамилии И.О.
2. Условия заданий, исходные данные для своего варианта переносятся в тетрадь.
3. Расчеты выполняются последовательно, с предварительной записью исходной формулы, разборчиво, окончательный результат заносится в ответ; перечеркивания, неаккуратные исправления не допускаются.
4. В необходимых местах проводить проверку решений, давать комментарии.
5. Эскизы выполняются только по линейке, желательно придерживаться требований ЕСКД, необходимые обозначения обязательны.
В целом, при выполнении заданий следует руководствоваться рекомендациями раздела 1.1 настоящего пособия.
2. ОБЗОР ОСНОВНЫХ МЕТОДОВ РЕШЕНИЯ ЗАДАЧ В ТОМД
2.1. Метод линий скольжения
Данный метод применяется для
решения плоских и осесимметричных задач. Метод интенсивно разрабатывался Генки
Г., Прандтлем Л. и Гейрингер Х. [1, 2]. На рис. 1 представлена схема
расположения линий скольжения в деформируемом теле и обозначения
геометрических характеристик. Траектории главных напряжений пересекают линии
скольжения под углом 
. Ясно,
что 
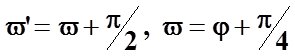, а потому можно
записать дифференциальные уравнения линий скольжения (линий Чернова - Людерса):
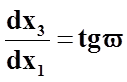(семейство 
), 
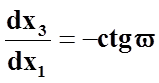(семейство 
).
При плоском
деформированном состоянии напряжения c учетом соотношения 
определяются
следующим образом:
(*)
 |
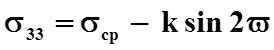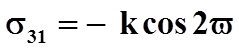
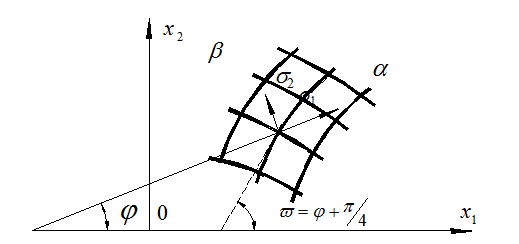Рис. 1 Траектории главных касательных напряжений
Для плоского деформированного состояния (*) условие пластичности выполняется тождественно:
.
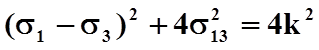Подставляя в уравнения равновесия значения напряжений (*) и переходя к криволинейным координатам, получим интегралы Генки:
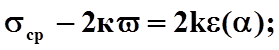
в которых 
, 
-
постоянны вдоль линий и соответственно.
Из двух последних уравнений можно получить разрешающее уравнение для определения напряжений:
.
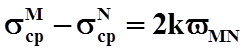Полученное уравнение позволяет утверждать следующее: если задана линия скольжения и среднее значение напряжения в одной точке, то можно найти среднее напряжение в другой точке, а следовательно, определить в точках выхода линий скольжения на контактные поверхности контактные напряжения и деформирующие усилия.
Условия на свободных и контактных поверхностях:
1) если сила трения
отсутствует, 
(линии скольжения
выходят на поверхность под углом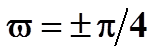 
);
2) при максимальном
контактном трении 
;
3) при промежуточных
значениях сил трения значение касательного напражения расположено в
пределах от нуля до 
.
Фактически, если удается построить подходящее поле линий скольжений, то задача определения деформирующих усилий практически решена. При построении полей линий скольжения используют их свойства.
Свойства линий скольжения
1. Линии скольжения непрерывны и образуют два семейства ор-
тогональных кривых.
2. Линии скольжения пересекают траектории главных напряжений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
