Теория обработки металлов давлением: Методические указания к решению задач, страница 8

7.2.2. Определить величину момента при изгибе упруго-пластического материала. Толщина полосы h, толщина упругой зоны .

7.2.3. Решить задачу 7.2.1 в предположении, что граница упругой и пластической зон соответствует деформации 0,2%.

7.2.4. В листовой штамповке получила широкое распростране­ние гибка поперечной силой. Считая заготовку идеально пласти­ческой, определить изгибающий момент и силу. Касательными на­пряжениями от перерезывающей силы пренебречь.

7.2.5. Для упруго-пластического изгиба полосы толщиной h и толщиной упругой зоны  определить радиус нейтрального сечения  и распределение деформаций. Считать, что геометрия изогнутой заготовки известна.

7.2.6. Построить эпюру остаточных напряжений и определить величину упругой деформации (так называемого пружинения) пос­ле пластического изгиба с упрочнением по линейному закону под действием остаточных напряжений [Д1].

7.2.7. Зарисовать эллипс пластичности, схемы напряженного состояния и знаки напряжений и  для подстановки в условие пластичности для операции вытяжки без утоне­ния, отбортовки, обжима и раздачи [5].

7.2.8. Построить поле линий скольжения по контуру вытяжки без утонения коробчатой детали с закруглениями в углах и контур ее оптимальной заготовки.

Указание. Зарисовывается контур четверти коробчатой детали в плане, определяются размеры заготовки на прямолинейных участ­ках и в углах как при гибке и вытяжке соответственно; затем строится комбинированное поле линий скольжения для угловой части контура, состоящее из трех полей. Контур заготовки пересекает линии скольжения под углом 45°.

7.2.9. Для случая вытяжки без утонения и без прижима по соответствующей формуле [5] вычислить величину  (с учетом трения и изгиба на радиусе матрицы) и усилия вытяжки. Величи­на ,размера заготовки и детали задаются преподавателем. 

7.2.10. Для гибки широкой полосы моментом вычислить  для значений  и построить соответствующие графики. Считать, что изменение толщины заготовки в очаге деформаций отсутствует.

 7.2.11. Для широкой полосы при гибке моментом вычислить:

·  Деформации окружные по радиусу с шагом 0,2и построить эпюру.

·  Вычислить также напряжения с темже шагом и построить эпюру.

          Взять:

7.2.12. Заготовку шириной S0 = 4 мм  изгибают на радиус 10 мм.                                   Определить положение нейтрального слоя деформаций и напряжений.

7.2.13.  При изгибе полосы S₀ = 4 мм  из некоторого материала получено, что разрушение наружного контура происходит при внешнем радиусе R=6мм. Считая поправочный коэффициент равным 1.12, определить относительное сужениеобразца из этого материала.

 7.2.14. При изгибе заготовки толщиной 5 мм  длина растянутого волокна относится к длине сжатого волокна на поверхнности материала в пределах угла , как .  Чему равна окружная деформация на расстоянии 1мм от наружного контура, если радиус нейтрального слоя деформаций   и составляет 16 мм.

 7.2.15. При гибке заготовки толщиной 2 мм пружинение составило     1.1 град. Материал Ст3. Каков угол гиба заготовки?

8. ЗАДАНИЕ НА РАСЧЕТНУЮ РАБОТУ ПО ТОМД

«Теория напряжений, деформаций, физические уравнения, условие пластичности»

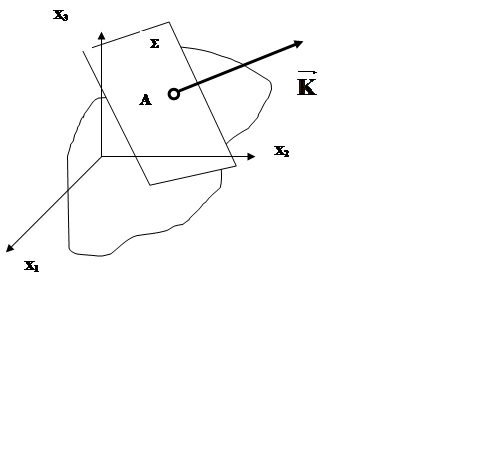
Заданы (табл.2):

·  Тензор Т_s в точке А;

·  Наклонная плоскость S,

     определяемая вектором ;

·  Модуль пластичности Е¢;

·  Предел текучести s_т.

Определить:

1.  Вектор напряжений, отнесенный к плоскости S.

2.  Нормальную и касательную составляющие вектора напряжений, отнесенные к плоскости S.

3.  Главные напряжения.

4.  Направляющие векторы площадок, к которым отнесены главные напряжения.

5.  Максимальное касательное напряжение, построив диаграмму Мора.

6.  s_{N  и}  s_t для точки, которой соответствуют значения a₁ =(см. зад.)  иa₃=(см. зад.). Здесь n_i=cos(a_i).

7.  Интенсивность напряжений в точке А в исходной системе координат и повернутой при отыскании главных напряжений.

8.  Состояние материала в точке А (упругое или пластическое).

9.  Главные деформации в точке А.

10.   Интенсивность деформаций.

11.   Проверить, выполняется ли условие несжимаемости в точке А.

12.   Вычислить показатель напряженного состояния для s_N = (s₁+s₂)/2.

                                                                                                      Таблица 2        

Таблица исходных данных для расчетов