Теория обработки металлов давлением: Методические указания к решению задач, страница 5

где

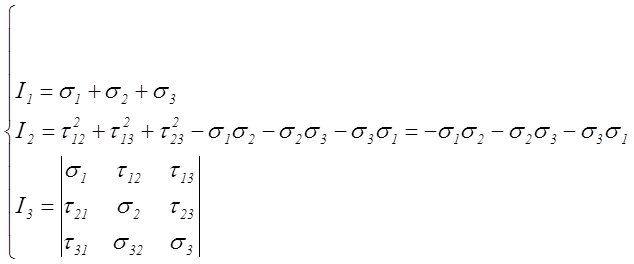
для заданного напряженного состояния имеем: .

Уравнение (1) принимает вид

                                                  

Левую часть этого уравнения можно разложить на множители

                                             

откуда

σ + τ = 0, либо .                                                        (2)

решая уравнение (2), найдем корни:

                                           σ = - t,   .

Для определения ориентации главных осей воспользуемся уравнениями :

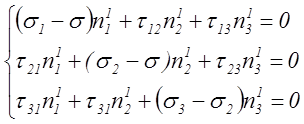                                                                  (3)

                                                                                      (4)

Подставив в систему (3) вместо значение , получим систему уравнений для  определения направляющих косинусов  первого главного направления. Исключив из первых двух уравнений, получим:

, .

Следовательно,  и в соответствии с  уравнением (4):

т.е. первое главное направление равнонаклонено к осям. Остальные направления определяются аналогично.

4.2. Задачи

4.2.1. Получить соотношение для объемных и логарифмических деформаций. Указать условие, при котором они совпадают. Найти различие между ними, если .

4.2.2.  Металлический куб растягивается вдоль одной из осей. Деформация в этом направлении . Найти относительное изменение объема куба, если коэффициент Пуассона равен . Откуда следует условие, что .

4.2.3. Стержень длинной 100 мм. Растягивают ступенчато до 104, 108 и 112 мм соответственно. Для данного случая проверить свойство аддитивности объемных и логарифмических деформаций. Найти различие и .

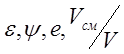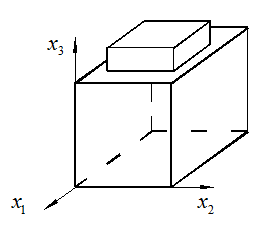
4.2.4. Образец длинной 80 мм, диаметром 80 мм растянут равномерно до 96 мм. Определить:  .     Указание: воспользоваться представлением деформации куба для вычисления смещенного объема.

                           Рис. 5.  Представление смещенного объема   

4.2.5. Вычислить скорость деформаций при осадке образца на молоте, скорость байка которого постоянна , в начале и в конце деформирования образца длиной 100 мм, при осадке на 20 мм.

4.2.6. Вычислить скорость деформации в начале и в конце деформирования, если известно, что длина образца в процессе деформирования изменялась по закону  (мм) суммарное время деформирования равно 1.5 сек. Определить скорость инструмента в конце первой секунды деформирования, а также вид процесса.

4.2.7. Вычислить скорость деформации заготовки высотой 100 мм при осадке  молотом простого действия, если высота подъема бойка 2.5 м. Вычисления отнести к началу процесса деформирования.

4.2.8.  Показать связь между  и  .

4.2.9. Первоначальная длина образца 50 (мм), конечная – 60 (мм). Найти .

4.2.10. С какой высоты должен падать молот, чтобы при осадке образца высотой 110 (мм) скорость деформирования составляла 50 1/с?

4.2.11. Деформируют заготовку длиной 100 (м) со скоростью инструмента, изменяющейся по закону: 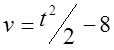 до достижения точки возврата процесса. Определить и е.

4.2.12. Определение вектора напряжений в системе базисных векторов, если его составляющие (2,3,1),используя правило суммирования Энштейна.

4.2.13. Определить проекцию вектора напряжения на ось,если его проекции на оси  и  равны 2 и 3,а его длина равна 5.

 4.2.14. Пусть дан тензор напряжений с компонентами . Как записать эти компоненты чтобы индексы были ш и к, т.е. . Доказать справедливость полученного соотношения для i=1; j=2.

4.2.15. Пусть площадка пересекает оси системы в точках (1,2,3). Каковы компоненты направляющего вектора?

4.2.16. Пусть две компоненты вектора напряжений  и равны 1 и 2

соответственно, а тензор напряжений, равен Т_s.  Найти компоненты направляющего вектора.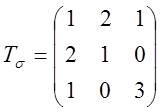

4.2.17.  Пусть компонента вектора напряжений на ось  равна 2, а компоненты тензора напряжений равны:;;. Найти проекцию направляющего вектора на ось ,если .

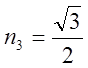4.2.18.  Закон парности касательных напряжений ,где тензор Леви-Чивиты. Записать закон парности касательных напряжений для i=1 и i=3.

4.2.19. При каких к будет иметь место плоское напряженное состояние, если .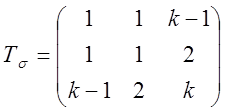

4.2.20.  Дан тензор 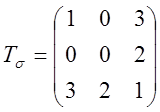. Найти главные напряжения.

4.2.21.  Элементы матрицы зависят от времени:             

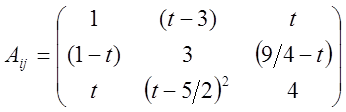
Определить момент времени, когда матрица может представлять собой тензор напряжений и записать его.

4.2.22. Направляющий вектор задан компонентами (1,3,2). Произвести нормировку данного вектора.

4.2.23. Найти компоненты вектора напряжений, если компоненты направляющего

вектора (3, 4, 0), а

                                               .

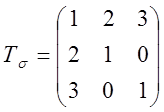4.2.24. Определить нормальное , касательное и полное напряжения на наклонной площадке , определяемой вектором (3,0,4) если .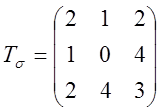

4.2.25. Направляющий вектор имеет компоненты (1,2,1), а компоненты вектора напряжений равны (5,2,1). Найти ,и угол между направляющим вектором и вектором напряжений.

4.2.26. Тензор напряжений имеет вид 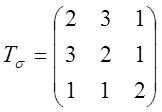, а направляющий вектор, расположенный в плоскости , делит угол между осями и  в соотношении 1:2, считая от оси . Найти .

4.2.27. Вычислить скорость деформации при осадке. На молоте в начальный момент и в конце осадки образцов, имеющих начальный размер по высоте 50, 100 и 200 мм, ход бойка молота в процессе осадки составил 20 мм, скорость в момент касания торца заготовки – 12 м/с. Какова зависимость скорости деформации от исходной высоты образца?

4.2.28. В результате испытания образца мягкой стали на одноосное растяжение из диаграммы напряжение – деформация получены следующие значения напряжений:

s, Мпа	0	2	5	10	20	100	200	240	280	320
e,%	0	0,1	0,25	0,50	1,0	0,50	1,0	20	40	60

Представить результаты испытаний графически и дать аналитическую аппроксимацию закона.

5. УСЛОВИЕ ПЛАСТИЧНОСТИ