Теория обработки металлов давлением: Методические указания к решению задач, страница 3

                        

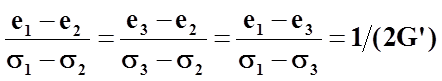
где G'  -  модуль пластичности,  который определяется экспериментально.

Предполагается, что  схемы  напряженного  и деформированного

состояний совпадают:

                                            ,

где   - показатель схемы напряженного состояния;

     - показатель схемы деформированного состояния.

Используется приближенное условие пластичности в виде:

                                             ,

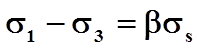где - показатель Лоде.

Например, если  из анализа формоизменения можно получить деформации, то из второго соотношения и определения схемы напряженного состояния получаем одно уравнение,  связывающее все три напряжения.  Второе уравнение доставляет нам приближенное  уравнение пластичности, а недостающее уравнение можно определить из условия равновесия выделенного объема как сумму напряжений  .   Переходя  от одного выделенного объема к другому,  можно определить поле напряжений в теле.  Процедура становится  особенно  простой, когда речь идет об определении напряженно-деформированного состояния частиц, расположенных вблизи поверхности.

2.6. Вариационные методы

Вариационные методы [12 - 14] определения усилий и деформаций,  как и метод баланса работ,  основаны на энергетическом принципе,  но  в отличие от метода верхней оценки и метода баланса работ позволяют определить не только полное и удельное усилия,  но и рапределение напряжений и деформаций по объему тела,  а также форму тела после деформации с учетом неравномерности деформации.

Вариационные методы основаны на положении: "сумма работ всех внешних и внутренних сил на возможных перемещениях около  состояния равновесия равна нулю".

Работа внешних сил ,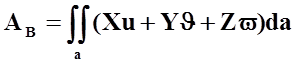

где X, Y, Z - компоненты  внешних поверхностных сил;

   u, , - компоненты перемещений.

Вариации работы внешних сил на возможных  пермешениях,  согласно уравнению для , определяются уравнением:

                   .

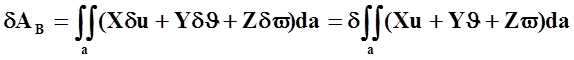 Вариации работы внутренних сил на  возможнцых  перемещениях, согласно уравнению для, определяются уравнением:

                                   .

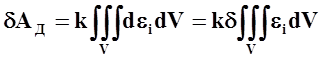В соответствии с принципом возможных перемещений,  учитывая, что  работа внутренних сил положительна,  а внешних отрицательна, имеем:

.

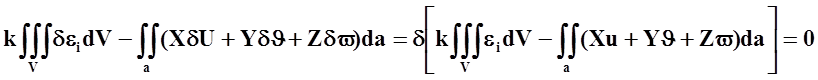Величина, стоящая в квадратных скобках,  представляет  собой полную энергию.  Следовательно, вариация полной энергии равна нулю. Это положение можно сформулировать так: "действительнкая форма равновесия тела отличается от всех возможных форм тем, что сообщает полной энергии минимальное значение".

Таким образом, задача может быть поставлена так: найти такую функциональную зависимость перемещений от координат,  при которой полная энергия принимает минимальное значение.

Решение практических задач обработки металлов давлением  методом вариационного исчисления представляет значительные математические  трудности.  Применением  приближенных,  так  называемых "прямых", методов вариационного исчисления удается решить большое число задач.

Один из прямых методов (метод Ритца) заключается в том,  что искомую функцию (применительно к обработке давлением этой функцией являются перемещения) представляют в виде ряда, например 

+ ...,

где , ,...,  - неопределенные параметры;

 (x,  y,  z),  (x, y, z), ... - функции координат, отвечающие граничным условиям.

Функции  можно принимать произвольно, лишь бы они отвечали граничным  условиям. 

В настоящее  время  вариационные методы используются большей частью при реализации их численных алгоритмов на ЭВМ (из-за  значительной трудоемкости вычислений).

   2.7. Метод конечных элементов

Метод конечных элементов впервые был применен Маркалом П.  и Кингом И. [15] для решения упруго-пластических задач. Учет контактных взаимодействий заготовки и инструмента учитывается с использованием различных моделей [16]. Суть метода заключается в разбиении тела на отдельные элементы, соединенные в узловых точках. Для каждого элемента решается полная система матричных уравнений механики сплошных сред,  опосредованная нелинейным функционалом,  для которого одним из методом оптимизации (линейное программирование, метод штрафных функций) отыскиваются решения,  приводящие  невязку к нулю.  Метод позволяет получать все характеристики напряженно-деформированного состояния, границы упругой и пластической областей,  перемещения и т.д.;  удовлетворительно работает при решении  задач  пластического  формоизменения осесимметричных заготовок и плоских задач. Решение задач в пространственной постановке (особенно при значительных размерах  заготовки  и при больших конечных деформациях) зачастую приводит процесс вычисления к расходимости.  Реализуется метод лишь на мощных ЭВМ, обладающих значительным быстродействием и ресурсами памяти.

3.  Физические основы пластической деформации

3.1. Примеры решения задач

3.1.1. Расстояние между атомами в направлении скольжения равно b. Расстояние между плоскостями скольжения равно a. Материал имеет простую кубическую решетку (a = b). Произошел сдвиг на одно межатомное расстояние. Модуль упругости E=2×10⁵ МПа.  Коэффициент Пуассона .

Чему равно значение критического скалывающего напряжения, если сдвиг осуществляется сразу по всей плоскости скольжения?

РЕШЕНИЕ. Согласно закону Гука Gx/a,где G - модуль сдвигa. Из периодичности касательного напряжения следует, что  Тогда  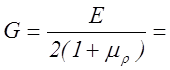8×I0⁴ МПа;   МПа. Данная задача может быть решена  в более точной постановке. По Я.И. Френкелю при скольжении по кристаллографическим плоскостям касательное напряжение является периодической функцией смещения х:

.

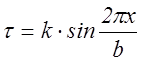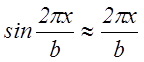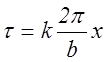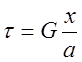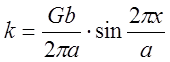При малом смещении ,  поэтому  (*). Согласно предыдущей задаче  (**). Приравнивая выражения (*) и (**), имеем ;  при  .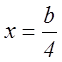

 Так как 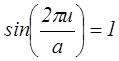     и  a = b, то .

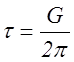Эксперименты показывают , что скольжение происходит при , что противоречит физической модели. Данное противоречие объясняется дефектами в металле.