Другие предметы \ Теория обработки металлов давлением

Теория обработки металлов давлением: Методические указания к решению задач, страница 4

ОТВЕТ: В приближенной и точной постановке задачи скалывающие напряжения отличаются друг от друга в два раза, однако это значение более, чем на три порядка отличается от скалывающего напряжения, возникающего в реальных металлах.

3.1.2. Межатомные силы имеют электромагнитную природу. Поэтому сила взаимодействия между двумя атомами в металле равна: 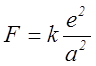, где  заряд электрона, межатомное расстояние . Определить теоретическую прочность стали.

РЕШЕНИЕ.  Число атомов, приходящихся на единицу площади равно 1/а.

Поэтому теоретическая прочность 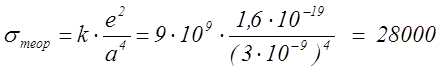  МПа.

Модуль упругости для стали Е=200000 МПа. Следователь­но, теоретическая прочность .

ОТВЕТ: Теоретическая прочность составляет 0,14 модуля упругости.

3.1.3. Образец стали длиной 80 мм и диаметром 8 мм растянут без образований шейки, т.е. равномерно, до длины 96 мм.

Вычислить следующие характеристики деформации: относитель­ное удлинение e, относительное сужение Y, логарифмическую деформацию и относительный смещенный объем в направлении растя­жения

РЕШЕНИЕ:  

                  

                           

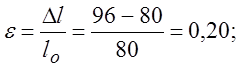
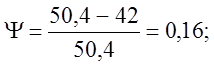
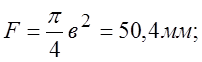
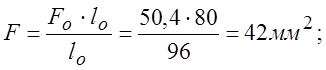
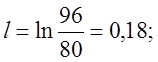
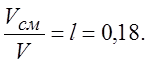
3.1.4. Построить графики зависимости скорости деформации по мере осадки образцов с начальной высотой 100 и 200 мм на кривошипном прессе со степенью относительной деформации 50 и 10%. Пресс имеет - 60 ходов в мин., радиус кривошипа R=150 мм, отношение длины шатуна к радиусу кривошипа К=0,186.

Определить графически среднее интегральное значение скорости деформации.

РЕШЕНИЕ; Скорость движения ползуна кривошипного пресса изменя­ется по закону

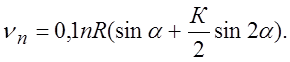
Здесь n- число оборотов коленчатого вала в мин, равное числу ходов пресса; R - радиус кривошипа, a -угол поворота колен­чатого вала. Скорость деформации 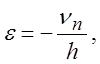 h –высота заготовки, изменяющаяся в процессе осадки, где - начальная высота,  - уменьшение высоты, равное величине хода ползуна на рассматриваемый момент осадки

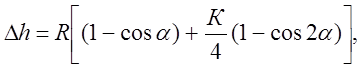
здесь 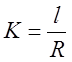 - отношение длины шатуна к радиусу кривошипа.

Итак,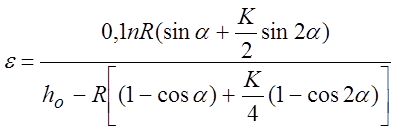

При известной  угол  определяется

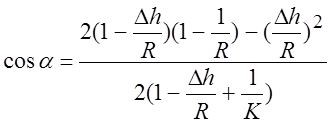
При h=100 мм, =50%, =50 мм, и если К=0,186, то угол  отвечающий рабочему ходу осадки определится

, 

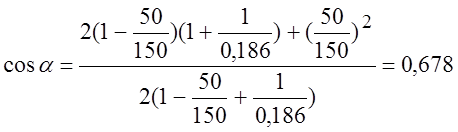Скорость деформации наначало осаждения

                                 

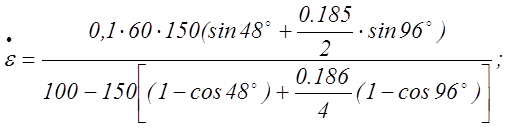
Далее аналогично вычисляют  для мм и строят график зависимости   и делением площади под кривой на общее перемещение получают среднее интегральное значение скорости деформации.

3.1.5. Вычислить величину удельного усилия и значение напряжения текучести способом измерения твердости на приборе Бринелля, если дано: диаметр шарика (D) 10 мм, диаметр отпечатка (d) 3,2 мм, усилие (Р) 10 кН.

РЕШЕНИЕ:  Согласно решению задачи вдавливания сферического пуансона в пластическое полупространство методом линий скольжения [3], удельное усилие определяют по формуле:

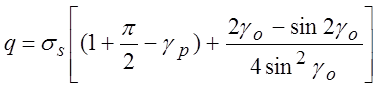
здесь  - половина угла, образованного дугой касания сферы внедренного пуансона с деформированным металлом.

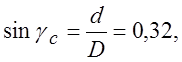
  рад.

С другой стороны 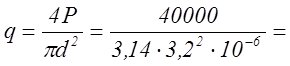1250 МПа

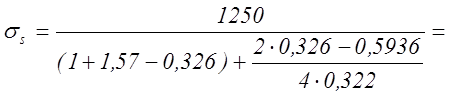494 МПа

ОТВЕТ: Удельное усилие составляет 494 Мпа.

3.2.  Задачи

3.2.1.  Найти предельную скорость деформации сдвига, если плотность дислокаций равна r = 1013 1/ м2. Вектор Бюргерса равен b = 3х10 мкм, скорость звука в металле равна 5000 м/с.

   3.2.2. Сталь с содержание углерода 0,45% при температуре 600С имеет предел прочности  300 МПа и при температу­ре 1200°С 30 МПа. Используя эти данные, записать выражений температурного закона Н.С. Курнакова.

3.2.3. До методике, изложенной в книге [9, с. 62-66] опре­делить сопротивление деформированию и пластичность сталей с содержанием углерода 0,15% и 0,42% (с. 54) для температуры 8000 , и для стали с содержанием 0,55% С (табл. 5, с. 65) при t=1100°С, скорости деформации 100 1/с степени дефор­мации e = 30%.

3.2.4. По диаграммам пластичности [9, с. 54,55,56] определить предельные значения показателей пластичности при температурах холодной и горячей штамповки для сталей, меди, дюралюмина, сплавов, АК6, ВТ3.

3.2.5. На основании диаграммы состояния и диаграммы пластичности для сталей с содержанием углерода 0,14% и 0,42% [9, с. 54,59] установить температурный интервал горячей обработки давлением, а по диаграммам рекристаллизации - примерную величину зерна, которая получится в результате обработки сталей при температурах начала и конца обработки со степенью деформации 35% [9, с. 41,75].

3.2.6. Работает источник Франка-Рида. Оценить величину скалывающего напряжения, необходимого для его действия;  G = 76500 Мпа, b = 3×10-10 м. Радиус кривизны источника – 1 мкм.

3.2.7. Изобразить плоскости и записать их обозначения, считая х1 = 1.

№

x2

x3

1

1/10

4/9

2

1/9

4/7

3

1/8

4/5

4

2/4

3/8

5

1/6

3/7

6

1/5

3/5

7

2/8

6/8

8

1/3

2/7

9

2/4

2/5

10

2/3

2/3

11

2/5

2/4

12

2/7

1/3

13

2/9

2/8

14

6/8

1/5

15

3/5

1/6

16

3/7

1/7

17

3/8

1/8

18

4/5

1/9


19

4/7

1/10

20

4/9

2/4

                                                                              Рис. 4 Кубическая решетка

4. ТЕОРИЯ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ

4.1. Примеры решения задач

Определить главные напряжения и ориентацию главных осей для напряженного состояния:

                                         , 

РЕШЕНИЕ. Для определения главных нормальных напряжений воспользуемся кубическим уравнением Гамильтона-Кэлли:

,                                                              (1)

Скачать файл