Теория обработки металлов давлением: Методические указания к решению задач, страница 6

5.1. Примеры решения задач

5.1.1. Напряжения в некоторой точке тела равны:  Может ли металл с пределом текучести  МПа находиться в упругом состо­янии?

РЕШЕНИЕ:  Используя условие пластичности, получим:

 

 МПа.    МПа.

Величина 116258>76832, следовательно, материал не может сохранить упругое сос­тояние.

5.1.2. Как изменится условие пластичности при растяжении образца в масле под давлением в 10 Мпа, если в обычных условиях предел текучести составляет 40 Мпа?

РЕШЕНИЕ: При испытании на растяжение материала при заданной степени деформации показал  Мпа, ().Наложим на схему растяжения шаровой тензор напряжения

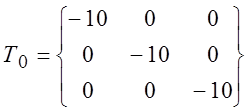 Получим

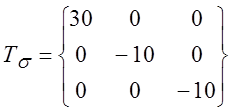
Вычислим из условия пластичности: ; 1600+0+1600=;  2×1600=;  40 МПа.

При наложении шарового тензора по условию пластичности не меняется.

5.1.3. Авторы [2] полагают, что пластическое разрыхление можно характеризовать относительным остаточным увеличением объема , а его приращение  пропорционально приращению степени деформации сдвига: =. В момент образо­вания микротрещины , где  степень дефор­мации сдвига к моменту разрушения металла - пластичность; она зависит от, температуры, гидростатического давления (-) интенсивности касательных напряжений  коэффициента  и отношения, .

Определить пластичность (степень деформации сдвига) стали З0ХГСА с учетом  показателя схемы напряженного состояния и отношения по диаграмме пластичности (рис.3.1 [2]), если задан тензор напряжения.

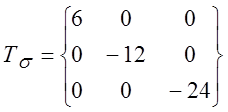
РЕШЕНИЕ: При испытании на растяжение, 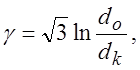  и  - диаметры образцов до и после испытания. При испытании на круче­ние ;  - угол наклона образующих линии после ис­пытаний к оси образца.

 ;

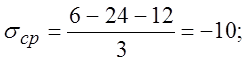
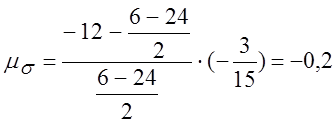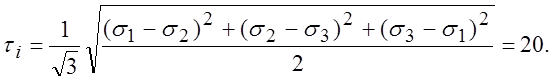
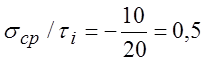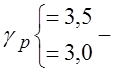; по диаграмме пластичности;

; ;

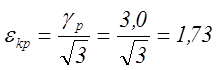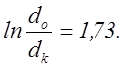
5.1.4. Для тензора напряжений Т_s вычислить  интенсивность напряжений s_i и среднее напряжение Р,  вычислить отношение s_i/P. Записать шаровой тензор T_s и тензор-девиатор T_D.

                                                   

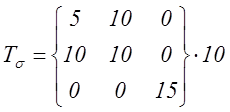
РЕШЕНИЕ:

;

                                              ; ;

 .

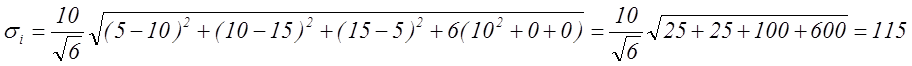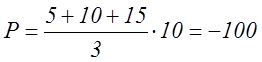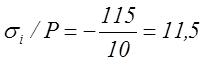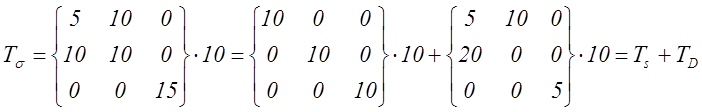5.2. Задачи

5.2.1. Напряжения в данной точке тела: , Каким пределом текучести должен обла­дать металл, чтобы при заданных напряжениях находиться в упру­гом состоянии?

5.2.2. Напряжения в данной точке свинцового образца равны . Напряжение текучести  МПа. В каком состоянии находится металл?

5.2.3. Показатели схемы напряженного состояния [7]:

                                               .

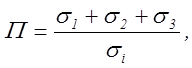
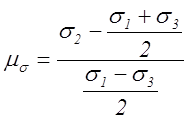Их величины характеризуют схему напряженного состояния и определяют пластичность материалов при данных условиях деформирования. Вычислить значения показателей П и m_s схемы напряженного сос­тояния для растяжения, сжатия, кручения и изгибе.

5.2.4. Задан тензор напряжений,

                                               

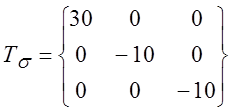
определить показатели П и m_s. По величине П к рис. 26 [7] определить величину критического значения деформации сдвига для стали У10А.

5.2.5. Стальная деталь нагружена и замерены компоненты тензора деформации:

.

Модуль пластичности  МПа, - коэффициент поперечной деформации. Величина среднего нормального напряжения  МПа. Записать тензор напряжений и разложить его на шаровой тензор и тензор-девиатор, пояснить роль каждого из них в упруго-пластической деформации.

Указание: Необходимо использовать зависимости между напряжениями и деформациями вида:            .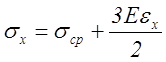

5.2.6. Задан тензор напряжений

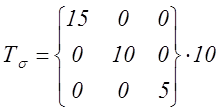
Вычислить величину интенсивности напряжений (). Раскрыть физический и математический смысл этого понятия. Записать в общем виде зависимость между интенсивностью () и интенсивностью (в пластической области) деформации (),раскрыть смысл коэффициента пропорциональности и метод его определения.     

5.2.7. Получить соотношение между обычной и логарифмической деформации и сделать вывод относительно их использования в условии пластичности, учитывающем упрочнение.

5.2.8. Выразить параметр Лоде через главные значения девиатора напряжений.

5.2.9. Преобразовать условие пластичности Мизеса с учетом перехода к главным напряжениям.

5.2.10. Считая, что главные оси тензора деформаций совпадают с главными осями тензора напряжений, записать соотношения пропорциональности между напряжениями и деформациями.

5.2.11. Записать связь девиатора тензора напряжений и интенсивности касательных напряжений.

5.2.12. Проверить, что для уравнений характеристик в методе линий скольжения условие Мизеса выполняется автоматически.

5.2.13. При каком значении параметра Лоде критерии Треска и Мизеса совпадают?

5.2.14. Записать условие пластичности Мизеса для плоского напряженного и плоского деформированного состояний.

5.2.15. Доказать, что если уравнения Прандтля-Рейсса выполняются, то выполняется и условие несжимаемости материала при пластической деформации.

6. АНАЛИЗ ОПЕРАЦИЙ КОВКИ И ОБЪЕМНОЙ ШТАМПОВКИ

6.1. Примеры решения задач

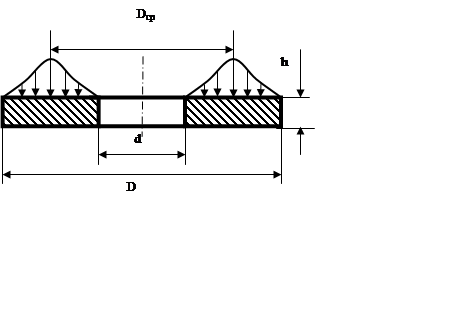6.1.1. Определить величину удельного усилия при осадке диска с отверстием (рис. 6) при значении коэффициента контактного трения [9], используя решение методом тонких сечений по аналогии с осадкой в кольцах [9]. Размеры диска: D=40 мм; d=20 мм; h=45 мм; напряжение текучести [9].

                                            Рис. 6. Осадка диска с отверстием

РЕШЕНИЕ: Совместное решение уравнения равновесия и условия пластичности на участке от 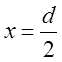 до 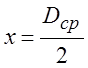 (рис. 6) позволяет получить величину  нормального к кон­тактной поверхности напряжения 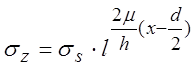 , на участке от  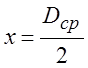до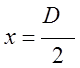

.

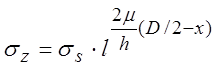На основании этих уравнений строится эпюра распределения нор­мальных напряжений на контактной поверхности. Через среднее зна­чение  удельное усилие выразится 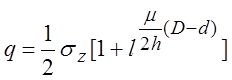, через среднее интегральное значение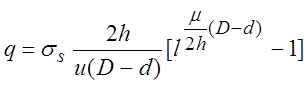

Вычисление по первой формуле дает величину q  =  1,43, по второй –

q  = 1,37 .

6.1.2. Используя метод верхней оценки получить формулу для определения величины удельного усилия (q) для начального этапа протяжки плоскими бойками.