Теория обработки металлов давлением: Методические указания к решению задач, страница 2

под углом .

3. 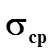   пропорционально углу поворота поворота линии.

4. Угол  между  касательными к двум линиям скольжения одного семейства в точках пересечения их каждой линией скольжения другого семейства остается постоянным (первая теорема Генки).

   5. При перемещении точки вдоль линии скольжения  одного  семейства  радиусы  кривизны  линий  скольжения другого семейства в точках пересечения с данной линией изменяются на  величину  пройденных расстояний (вторая теорема Генки).

   6. Угол наклона линий скольжения на контуре зависит от касательных напряжений.

   В общем случае,  линии скольжения, построенные на основе вышеуказанных свойств,  должны удовлетворять кинематическим условиям. Итак, построение полей линий скольжения позволяет определять деформирующие усилия при обработке металлов давлением.  Метод может быть использован для следующих процессов:  волочение, вдавливание,  рубка, протяжка, обжатие, изгиб, прокатка, прямое (обратное, боковое) выдавливание.

   2.2. Инженерный метод и метод прямого интегрирования

   Оба метода применяются для решения широкого класса плоских и осесимметричных задач: деформирование трубчатых заготовок в условиях внутреннего, внешнего или комбинированного давления; сжатие полосы шероховатыми шероховатыми плитами; сжатие клиновой заготовки; формовка деталей конической формы; осадка толстостенной трубы в матрице.

   Оба метода позволяют находить распределение напряжений в деформируемой заготовке [1 - 7]. Метод прямого интегрирования является более общим,  хотя и для получения аналитических решений требуется существенное упрощение исходных уравнений на основе разумных  допущений  о характере протекания процесса формоизменения. В том и другом методе в ряде случаев удается найти и распределение  деформаций (в инженерном методе для этого необходимы дополнительные данные, возможно, экспериментальные).      Используемые в  обоих  методах  уравнения и условия даются в табл. 1.

                                                               Таблица 1

Сравнительная характеристика  двух методов

Инженерный метод		Метод прямого интегрирования
1)Уравнения равновесия 2)Условия пластичности 3)Граничные условия		1) Уравнения       равновесия 2)  Условия           пластичности 3)  Физические уравнения 4)  Уравнения неразрывности 5)  Граничные условия

   2.3. Метод верхней оценки

   Метод разработан Джонсоном В. и Кудо Х.[1, 5]. Суть метода состоит в том, что объем очага деформации заменяется набором жестких блоков, т.е. производится замена поля линий скольжения (действительного) системой прямолинейных отрезков.  Блоки представляют  собой треугольные призмы

(см. рис. 2). Внутри каждого блока скорость постоянна.  Число и размеры блоков первоначально выбирают  произвольно.  Вдоль границ касательные напряжения берут максимальными:;  на свободной поверхности ; на контактных поверхностях   .

   Мгновенная мощность внутренних сил:

                                           ,

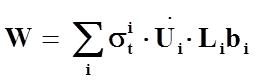где   - касательные напряжения;

   - скорость скольжения вдоль границ;

    - длины стороны треугольников при плоской деформации;

    - длина проекции площадки контакта в направлении x₁.

   Мгновенная мощность на пуансоне:

                                                .

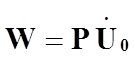   Здесь      - скорость движения пуансона,

                Р - полное усилие деформирования.

   Приравняв правые части мгновенных мощностей в  деформируемом теле и на пуансоне, получим:

                                .

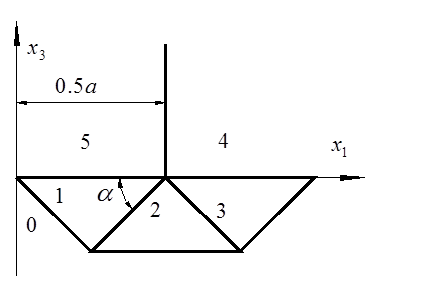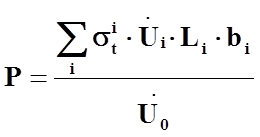                           Рис. 2. Разбиение заготовки на блоки

   Скорости определяются из годографа скоростей (рис.3).Удельное усилие  q

 (при  = const):

                                      

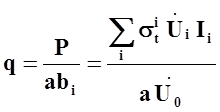
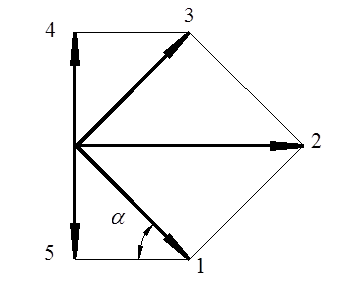                             Рис. 3. Годограф скоростей

   Этот метод может использоваться для квазистатических процессов в случае не слишком больших деформаций при расчетах процессов ковки,  штамповки,  осадки, прямого, обратного и комбинированного выдавливания.  Метод не позволяет выявлять распределение напряжений.

   2.4. Метод баланса работ

   Данный метод [1, 3, 5, 6, 8 - 10] основан на законе сохранения энергии,  согласно которому работа внешних сил на соответствующих  перемещениях равна работе внутренних сил деформирования:

                                           ,

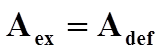где  -  работа внешних сил;

       - работа внутренних сил деформирования.

При этом упругая деформация не  учитывается,  материал  заготовки считается несжимаемым, а работа внутренних сил определяется через интенсивности деформаций сдвига и касательных напряжений   и  :

                                         .

Полная работа деформирования тогда определяется тройным  интегралом:

                                        .

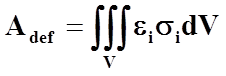Работа внешних сил определяется  интегральным выражением:

                                     

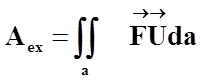
где  - вектор поверхностных  сил,  действующих  на  элементарную площадку  dа;

    - вектор перемещений.

   Данный метод может быть использован для определения деформирующих усилий при процессах  осадки,  ковки  и  объемной  горячей штамповки.  Он не позволяет находить распределение полей напряжений и деформаций.

2.5. Метод сопротивления пластическим деформациям

Этот метод [5,  9,  11] разработан профессором Г.А.  Смирновым-Аляевым для решения практических задач конечного формоизменения:  определения усилия по заданному формоизменению, определение деформаций по заданной нагрузке и работе внешних сил, определение формы тела на последовательных по конечной форме.  Процесс считается монотонным и зависимости между напряжениями  ,  ,   и конечными деформациями  , ,  записываются в виде: