Теория обработки металлов давлением: Методические указания к решению задач, страница 7

РЕШЕНИЕ: Используем типовое поле скоростей жестких треугольни­ков и городограф скоростей [1], показанные на рис. 2 и 3.

.

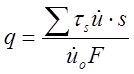Здесь ;   ;

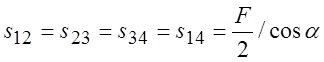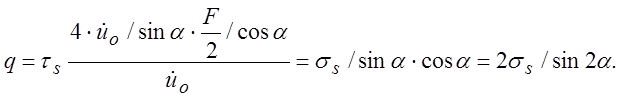
6.1.3. Определить сопротивление порога расширяющейся облойной щели при штамповке круглой в плане поковки.

РЕШЕНИЕ: 

.

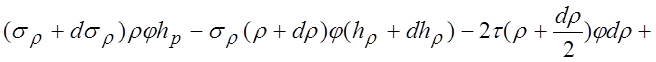
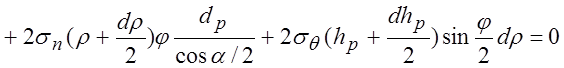Пренебрегая дифференциалами высоких порядков, приняв , , ,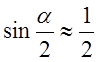

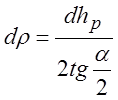получим:

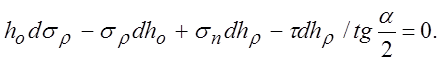
Если , а условию пластичности , то ,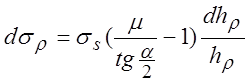

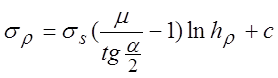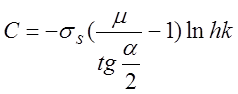а  . Если при ,  то , а

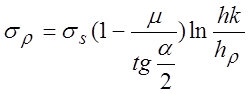. Из условия пластичности .

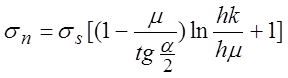Сопротивление порога облойной щели .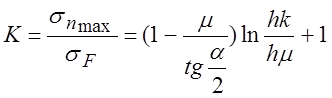

6.1.4. Методом баланса работ вывести формулу для определения усилия и удельного усилия при осадке полосы значительной длины между шероховатыми плитами, т.е. в условиях. Плоской деформации.

РЕШЕНИЕ: Уравнение баланса работ  или

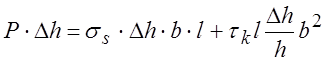; отсюда ;

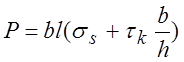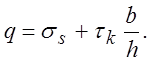
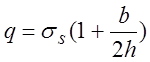При    ;      при     .

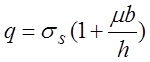6.1.5. Выполнить совместные решения уравнения равновесия и условия пластичности для случая пластической деформации сферы под равномерным наружным давлением, выделив представитель­ный объем в пористом теле в виде такой, сферы, получить зависимость относительной пористости  от гидростатического давления (P).

РЕШЕНИЕ: Уравнение равновесия в сферических координатах –

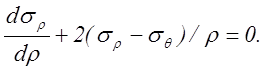
Условие пластичности:    

Подстановка второго в первое дает .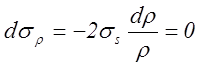

Граничные  условия: при , при .

Решение получится в виде: .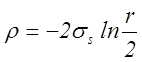

Отсюда           .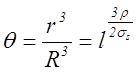

6.2. Задачи

6.2.1. Построить эпюру нормальных контактных напряжений, определить усилия (Р) и работы деформации (А) при осадке полосы, длина которой (L) значительно больше ширины (а), т.е. в условиях плоской деформации, при  используя метод тонких сечений.

6.2.2. В продолжение задачи 6.2.1 вычислить величину усилия и работы деформации, если дано; a=200мм; мм; L=1000 мм, МПа;  мм;  МПа.

6.2.3. Построить эпюру нормального контактного напряжения, определить величину усилит (Р) при осадке цилиндра (), используя метод совместного решения приближенных уравнений равновесия и условия пластичности.

6.2.4. В продолжение задачи 4.3 вычислить усилие деформации, если дано: d=200 мм, h=100 мм,  МПа; 0,4.

6.2.5. Определить величину работы деформации при осадке цилиндра, если величина удельного усилия .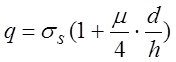

6.2.6. В продолжение задачи 5 вычислить величину paботы деформации при осадке цилиндра, если дано: d=30 мм, МПа; мм; мм.

6.2.7. Используя метод совместного решения уравнений рав­новесия к условия пластичности, вывести формулу для удельного усилия при протяжке и круглых вырезных бойках (решение см. в [5]).

6.2.8. Построить сетку линий скольжения и определить контактное нормальное напряжение при осадке тупого клина (рис. 7) без учета трения.

                        Рис. 7. Осадка тупого клина

6.2.9. Построить поле линий скольжения для схемы калибров­ки пористой цилиндрической втулки проталкиваниями через жест­кую матрицу, определить глубину очага пластической деформации (а) и при задании припуске на калибровку (), вычислить среднюю плотность пластически деформированного слоя () при известной начальной плотности ().

6.2.10. Построить сетку линий скольжения для случая внедрения пуансона в полупространство и вывести формулу для удельного усилия без учета трения.

   

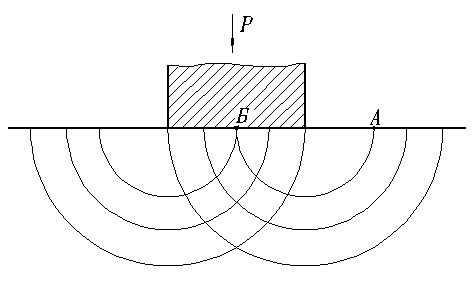  Рис. 8. Внедрение плоского пуансона в полупространство

6.2.11. Изучить пластическое течение в толстостенной трубе (рис. 9) под   действием внутреннего и внешнего давлений Р и q. Установить, при каких соотношениях геометрических параметров начнется пластическое течение.

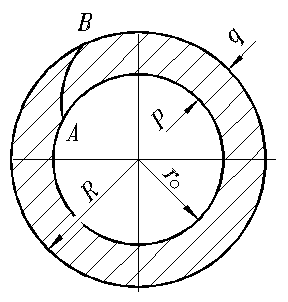                          Рис. 9. Течение материала стенок в трубе

7. АНАЛИЗ ОПЕРАЦИЙ ЛИСТОВОЙ ШТАМПОВКИ

7.1. Примеры решения задач

7.1.1. Определить величины напряжений и изменения толщины металла при разбортовке трубной заготовки с конуса на фланец методом совместного решения уравнения равновесия и условия пластичности без учета трения.

РЕШЕНИЕ: Вычертить расчетную схему разбортовки. Уравнение равновесия:

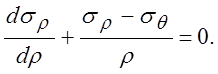
Условие пластичности с учётом знаков напряжений: .

Совместное решение при граничном условии (при )

 ,

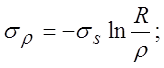
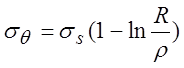здесь; R- наружный диаметр фланца разбортованной трубы, -радиус до центра радиусной части перехода от цилиндра к плоскому фланцу,  - радиус   выделенного элемента заготовки на плоской части фланца.   При

,  .

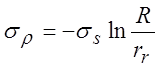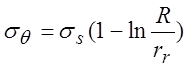При соотношения между напряжениями и деформацией принимает вид: .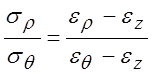

Если использовать условие постоянства объема , то можно выразить

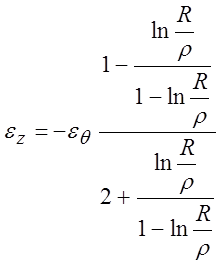
Если представить 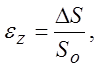 то изменения толщины  Далее необходимо вычислить, , ,  конкретного примера.                                                                                              

7.1.2. Определить радиус нейтральной линии при гибке широ­кой полосы изгибающим моментом, если дано: r=5 мм, s=2 мм.- толщина металла. Вычислить также длину заготовки, суммарная длина не охваченных пластической деформации участков равна 100 мм, а угол гибки 90°.

РЕШЕНИЕ: , длина дуги - 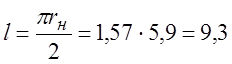 мм.

Длина заготовки мм.

7.1.3. Для операции вытяжки без утонения и без прижима определить величину напряжений во фланцевой части заготовки без учета упрочнения металла.

РЕШЕНИЕ [4]:

Уравнение равновесия -  .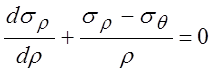

Условие пластичности    Совместное решение дает: ;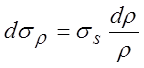

после интегрирования при граничном условии (при ) получаем:

                                 ;          

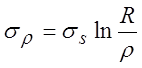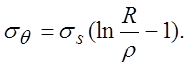
7.1.4. В продолжение задачи 7.1.3 вычислить предельное теоретическое значение коэффициента вытяжки.

РЕШЕНИЕ: Определив величину коэффициента вытяжки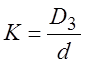

и используя выражение для  предыдущей задачи, приравня­ем и получим 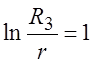,  k = 2,72.

7.2. Задачи

7.2.1. Записать формулы, определяющие изменение напряжение по высоте (одномерная задача) для случая чистого изгиба мате­риала: а) упругого, б) жесткопластического, в) упругого иде­ально пластического, г) уточняющегося по линейному закону, д) упругого и упрочняющегося по линейному закону, е) упругого и упрочняющегося по степенному закону, ж) упрочняющегося по степенному закону. Построить эпюры напряжений.