Другие предметы \ Тепломассообмен

Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 9

                              (3.55)

то с учетом определения скорости трения

получим

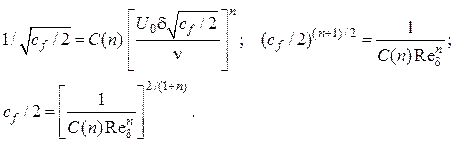       (3.56)

Значения C(n) в зависимости от показателя степени n были вычислены Вигхардтом [1]. При n = 1/7, C(n) = 8,74 можно показать, что формула (3.56) в точности соответствует широко известной эмпирической формуле Блазиуса, которая была получена при исследовании турбулентного течения в трубах при Red < 105. Для течения на пластине она имеет вид

                         (3.57)

Для течения в трубах ее записывают, как правило, в виде

             (3.58)

Следует иметь в виду, что при этом

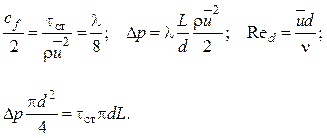
Здесь l – коэффициент гидравлического сопротивления;  – коэффициент трения (обе величины определяются по среднерасходной скорости ). Задаваясь степенным профилем, можно найти

, где U0 = Umax – скорость на внешней границе пограничного слоя (на оси трубы).

Формулы (3.57) и (3.58) полностью соответствуют друг другу с учетом приведенных соотношений и того, что Umax = U0  и d= 2δ. В общем же виде из формулы (3.57) с учетом соотношения для δ** / δ (3.52) следует закон трения в виде

                                   (3.59)

где

Значения параметров пограничного слоя со степенным профилем скорости для течения на пластине и в трубе приведены в табл. 3.1.

Т а б л и ц а  3.1

Параметры

n

1/7

1/8

1/9

1/10

C(n)

8,74

9,71

10,6

11,5

A

0,0128

0,0103

0,0095

0,0074

m

0,250

0,222

0,200

0,182

δ**/ δ

0,0975

0,0890

0,0818

0,0757

H

1,28

1,25

1,22

1,20

Формула (3.59) получена при турбулентном обтекании плоской пластины потоком несжимаемой жидкости с постоянными физическими свойствами. Как и при ламинарном течении, такие условия будем считать «стандартными» – при отсутствии воздействия на пограничный слой различных возмущающих факторов: неизотермичности, сжимаемости, вдува и т.д. Для этих условий коэффициенты трения и тепломассообмена  и  будем обозначать индексом «0».

Практически в области числа Re** < 104 можно пользоваться формулой для закона распределения скорости n = 1/7:

,                        (3.60)

а в области 104 < Re** < 106 – законом, где  n = 1/10.

На рис. 3.14 сопоставляются формула (3.60) и логарифмический закон сопротивления Кармана (3.47) с опытными данными по коэффициенту трения на плоской пластине [3].

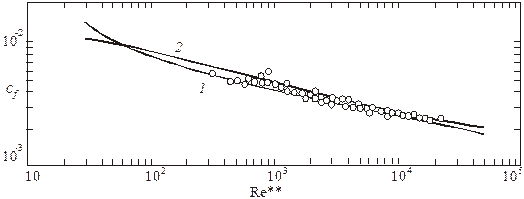
Рис. 3.14.  Закон трения для турбулентного пограничного слоя

на плоской пластине: 1 – расчет по формуле Кармана (3.47);

2 – расчет по формуле (3.60)

Для газов при Pr ≈ Sc ≈ 1, пользуясь аналогией процессов переноса импульса, энергии и массы (аналогией Рейнольдса), можно принять

                                  (3.61)


При Pr ≠ 1 и Sc ≠ 1 необходимо учитывать их влияние. В принципе существуют теоретические методы, основанные на анализе ламинарного подслоя, позволяющие получить влияние числа Pr. Но они достаточно громоздкие, и здесь мы их рассматривать не будем. Тем более, что достаточно непростые формулы потом аппроксимируются степенной зависимостью.

В диапазоне изменения Pr и Sc от 0,5 до 10 хорошие результаты дают формулы [2]:

        (3.62)

На рис. 3.15 сравнивается расчет по формуле (3.62) с опытными данными по теплообмену на плоской пластине в потоке воздуха.

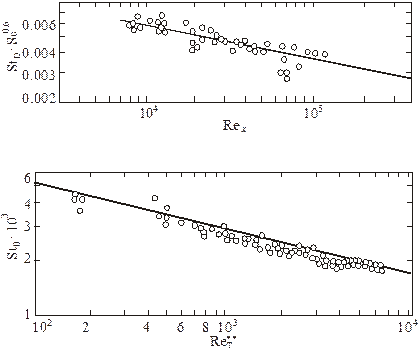
Рис. 3.15. Закон теплообмена на плоской пластине:

 (–) – расчет по формуле (3.62)

3.6. Решение интегральных соотношений

       турбулентного пограничного слоя

Как уже отмечалось, интегральные соотношения одинаково справедливы и для ламинарного, и для турбулентного пограничных слоев, поскольку представляют собой балансовые уравнения переноса импульса, энергии и вещества для рассматриваемого элемента пограничного слоя. При этом их можно получить как из дифференциальных уравнений, так и путем составления баланса для элементарного участка пограничного слоя. Поэтому уравнения импульса и энергии сохранят свой прежний вид.

Уравнение импульсов

                (3.63)

Уравнение энергии

                  (3.64)

Здесь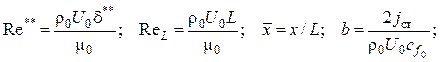    

 – проницаемость; – относительный коэффициент трения или тепломассообмена, характеризующий влияние различных возмущающих факторов (неизотермичность, вдув и т.д.) по сравнению со «стандартными» условиями. Хотя сами интегральные уравнения остаются такими же, как и для ламинарного слоя, но их решения будут другими, поскольку в этом случае другие законы трения и теплообмена ( и Ψ).

Как мы помним, в общем случае для турбулентного пограничного слоя получен логарифмический закон трения. Однако введение в интегральные соотношения (3.63) и (3.64) степенных законов трения и тепломассообмена типа (3.60) и (3.62) позволяет получить более простые аналитические решения.

Скачать файл