Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 8

Логарифмический закон трения. Закон трения для турбулентного пограничного слоя будем искать, как и для ламинарного, в виде зависимости

с_f /2 = f (Re^**).

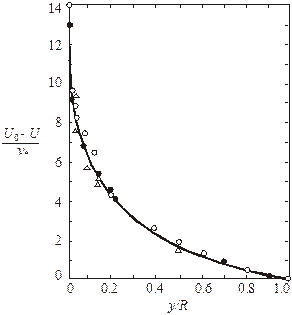
Рис. 3.12.  Закон дефекта скорости в сравнении

с экспериментальными данными

Он следует из логарифмического профиля скорости, который для условий на границе пограничного слоя (3.38) при у = δ, u = U₀ примет вид

.

С учетом того, что  получим

или

                              (3.41)

где

                       (3.42)

Характерные толщины пограничного слоя:

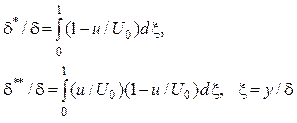           (3.43)

определим с учетом полученного выражения (3.39) для дефекта скорости:

(U₀ – u)/v^* = – 1/æ ln x    или   u/U₀ = 1 + (1/æ);

 = (–1/æ) ;

d^* / d = (–1/æ)(–1/æ)       (3.44)

= (1/æ)

d^** / d = (1/æ)/æ².                         (3.45)

Подставив (3.45) в (3.42), определим С_*:

С_* = 5,5 + (1/æ) ln (æ²/æ)

При больших числах Рейнольдса  æ = 0,4 >>

С_* = 5,5 +2,5 ln 0,4 = 3,21

и окончательно логарифмический закон сопротивления (3.41) примет вид

                           (3.46)

В области умеренных чисел Рейнольдса более точные результаты дает формула Кармана

`                            (3.47)

3.5.2. степенные профили скорости

С расчетной точки зрения во многих случаях, особенно при решении интегральных соотношений, степенные профили скоростей и законы трения более удобны, чем логарифмические.

Логарифмический профиль скорости

j = (1/æ) ln η + с                                   (3.48)

является огибающей семейства степенных профилей

j = С(n) ηⁿ.                                         (3.49)

При этом зависимость (3.49) представляет собой степенную аппроксимацию универсального логарифмического профиля (3.48) в некотором интервале числа  Re^** (см. рис. 3.11).

Коэффициент С(n), зависящий от n, и показатель степени n вычисляются из условия соответствия степенного профиля логарифмическому.

Выражению (3.49) с учетом того, что

          (3.50)

соответствует и более простое степенное выражение

                          (3.51)

откуда следует, что

        (3.52)

При выводе логарифмического закона трения с использованием выражения для дефекта скорости

u/U₀ = 1+ (1/æ)

мы получили [см. (3.44)], что

= (1/æ)                                  (3.53)

тогда из (3.53) и (3.52) имеем

n/(1 + n) = (1/æ)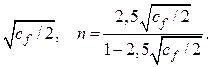               (3.54)

Как видно из формулы (3.54), показатель степени n должен уменьшаться с ростом числе Re, поскольку коэффициент трения уменьшается. Но если c_f зависит от числа Рейнольдса достаточно слабо, показатель n остается почти постоянным в практическом диапазоне чисел Рейнольдса. Степенной профиль скорости ω = ξ^1/7 для турбулентного пограничного слоя сначала был получен экспериментально. Причем эта зависимость описывает экспериментальные профили в очень широком диапазоне чисел Рейнольдса до Re^** < 10⁴. Это подтверждает вывод из формулы (3.54) о слабой зависимости n(Re). Поэтому для турбулентного пограничного слоя закон «одной седьмой» получил очень широкое распространение. На рис. 3.13 сравниваются профили скорости в турбулентном и ламинарном пограничном слоях. При экспериментальном определении показателя степени n следует пользоваться не формулой (3.51), а интегральными характеристиками δ^* и  δ^** (3.52), учитывая, что Н = 1 + 2n; погрешность, как правило, невелика.

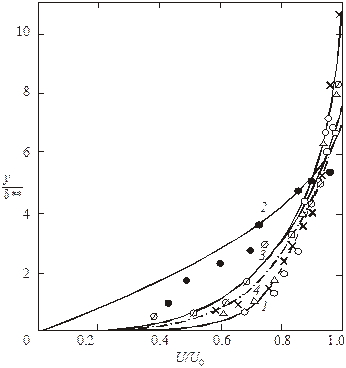
Рис. 3.13. Cопоставление опытных профилей скорости

с теоретическими зависимостями: 1 – распределение скоростей

U/U₀ = (y/δ)^1/7; (○, Δ, х) – опыты при турбулентном режиме,

Re_x = (4…5) 10⁵; 2 – ламинарный профиль Польгаузена

U/U₀ = 2(y/d) – 2(у/d)³ + (у/d)⁴; (●) – эксперимент

при   ламинарном   режиме,   Re = 1,5 10⁵;

3 – теоретические зависимости для пограничного слоя

со вдувом; (Æ) – соответствующие опыты [5]

Степенные законы трения и тепломассообмена. Степенному профилю скорости соответствует и степенной закон трения.

Если записать профиль скорости (3.49) для условий на внешней границе пограничного слоя при у = δ; u = U₀