Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 2

В пограничном слое на пластине формпараметр уменьшается от Н_л » 2,6 в ламинарной области до значения Н_т » 1,4 в турбулентной (рис. 3.3).

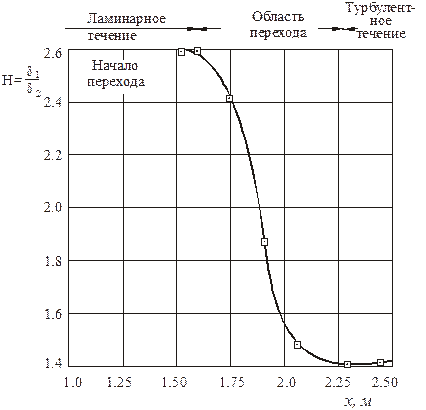
Рис. 3.3. Изменение формпараметра при переходе

ламинарного течения  в турбулентное

В инженерных расчетах обычно принимают, что переход от ламинарного пограничного слоя к турбулентному на пластине происходит в диапазоне (Rе_х)_кр = (2…5) 10⁵. Эти данные относятся к обтеканию гладких поверхностей с достаточно высокой турбулентностью внешнего течения.

Число Re_x не очень удобно использовать в качестве критерия перехода от ламинарного пограничного слоя к турбулентному, поскольку в него входит постоянная скорость внешнего течения U₀ . Если U₀ существенно изменяется по х, то использование  Re_x  лишено физического смысла.

Предпочтительнее иметь местный параметр перехода, напри-мер число Рейнольдса, в которое входят локальные характеристики пограничного слоя. Линейным размером может служить условная толщина слоя, однако она  не всегда может быть найдена из-за нечеткого ее определения. Поэтому за линейный размер можно принять интегральные величины: толщину вытеснения или толщину потери импульса .

Для ламинарного течения на пластине из интегрального соотношения импульсов следует, что

 .                        (3.1)

Если принять, что при обтекании плоской пластины

, то с учетом (3.1) получаем

.                        (3.2)

Соотношение (3.2) является местным критерием перехода от ламинарного пограничного слоя к турбулентному независимо от предыстории течения.

Вычислим для ламинарного течения в трубе критическое значение числа Рейнольдса , рассчитанное по скорости на оси трубы (при ) и по толщине потери импульса.

, где .

Для ламинарного слоя , тогда для трубы

.                                          (3.3)

Интересно отметить, что критические значения такого числа Рейнольдса близки для пластины и трубы. Таким образом, предложенный критерий удовлетворителен, по крайней мере, с этой точки зрения.

Значение Re_кр в общем случае зависит от большого числа факторов. Ограничиваясь учетом наиболее важных, можно записать

.

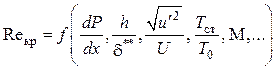Это выражение показывает зависимость Re_кр от величины продольного градиента давления, относительной шероховатости , степени турбулентности потока, температурного фактора и числа Маха. Более детальную информацию о влиянии этих факторов на Re_кр можно найти в книге Шлихтинга.

3.2.  Осредненное и пульсационное движения.

        Дифференциальные уравнения турбулентного

        пограничного слоя (уравнения Рейнольдса)

Исследования турбулентного потока показывают, что в каждой фиксированной точке потока скорость, давление и температура не ос-таются постоянными во времени, а очень часто и неравномерно изменяются (рис. 3.4). Такие изменения называют пульсациями,и они являются наиболее характерным свойством турбулентного течения.

t

 

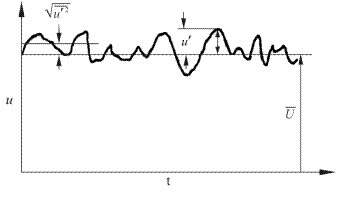
Рис. 3.4. Изменение скорости турбулентного течения

по времени. U – средняя составляющая скорости;

 u¢ – пульсационная составляющая скорости

(относительно среднего значения)

Чтобы получить уравнения сохранения для турбулентного потока, заменим мгновенные значения параметров, входящих в уравнения движения и энергии, суммой средней и пульсационной составляющих этих параметров. Например, скорость и плотность записываются следующим образом:

где u и ρ – полные, или мгновенные, значения скорости и плотности; и  – наложенные пульсационные составляющие, а  – осредненные по времени значения скорости и плотности.

Осредненное по времени значение переменного параметра f(t) определяется соотношением

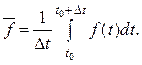
Чтобы осреднение не зависело от времени, необходимо правильно выбрать интервал времени Δt, который должен быть достаточно большим по сравнению с периодом пульсаций, но и достаточно малым по сравнению с каким-либо характерным для  осредненного движения интервалом времени, чтобы не учитывать возможных изменений средних параметров потока во времени.