Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 4

        и теплопроводность

        при турбулентном движении

Действие пульсационного движения на осредненное проявляется как бы в увеличении вязкости осредненного течения. Можно провести качественную аналогию между турбулентной вязкостью и молекулярной, если вспомнить, что молекулярная вязкость возникает в результате наложения хаотического теплового движения молекул на упорядоченное движение жидкости, а турбулентная есть результат наложения пульсационного движения на осредненное.

Дадим наглядное качественное пояснение появлению дополнительной турбулентной вязкости и теплопроводности с помощью теоремы импульсов.

Пусть в пограничном слое распределения скорости и и температуры Т заданы некоторыми функциями от  у: и = и(у), Т = Т(у).

Рассмотрим единицу площади поверхности в плоскости X – Z, перпендикулярной оси у (рис. 3.6). Через эту площадку протекает газ массой m = ρv. Перетеканию жидкости соответствует некоторый поток импульса, проекция которого на ось х

у_х = mu = ρvu.                                       (3.8)

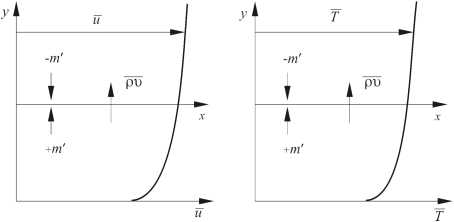
Рис. 3.6. К выводу соотношений для дополнительного

турбулентного трения τ_t и  теплового потока q_t

Будем рассматривать пульсацию потока массы вдоль оси у m¢ = = (ρv)¢. При наличии пульсаций проекция на ось х потока импульса через ту же площадку:

                 (3.9)

После осреднения за достаточный промежуток времени получим

,                          (3.10)

так как 2-й и 3-й члены в выражении (3.9) после осреднения равны нулю.

Как видно из сравнения соотношений (3.8) и (3.10), при наличии пульсаций появляется дополнительный перенос импульса

При переносе импульса от слоя к слою происходит изменение импульса этих слоев (увеличение или уменьшение). Это означает, что на каждый из слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона). Сила эта, отнесенная к единице площади поверхности, есть не что иное, как сила трения между слоями газа. Или, другими словами, можно сказать, что поток количества движения, передаваемый в соседний слой жидкости через площадку, эквивалентен противоположно направленной силе, с которой этот слой действует на площадку.

Следовательно, при наличии турбулентности (пульсаций скорости) возникает дополнительное напряжение трения между слоями жидкости

                                       (3.11)

Аналогично можно показать, что при существующих пульсациях температуры поток теплоты через единичную площадку равен

                             (3.12) и что при этом возникает дополнительный турбулентный перенос энергии

                                        (3.13)

Легко убедиться в том, что значения τ_t и q_t не равны нулю. Если жидкости, попадающие вследствие поперечного движения в слой у снизу  движутся из области с меньшей средней  скоростью ū, то в слое у  они вызывают отрицательную пульсацию  таким образом,  Точно таким же рассуждением можно показать, что и для частиц, проникающих в слой у сверху,  Следовательно, и среднее значение не равно нулю и имеет отрицательный знак . Это означает, что турбулентное касательное напряжение положительно  и совпадает с «ламинарным» касательным напряжением.

Используя эти результаты, можно ввести понятие турбулентной вязкости μ_t и теплопроводности λ_t. По аналогии с ламинарным течением

,                              (3.14)

.                           (3.15)

Подобно тому, как в случае ламинарного движения, связь между молекулярными процессами переноса импульса, теплоты и вещества количественно характеризуется числами Прандтля и Шмидта:

в случае турбулентного течения вводят их аналоги – турбулентные числа Прандтля и Шмидта. Например, турбулентное число Прандтля