Турбулентный пограничный слой. Переход ламинарного течения в турбулентное, страница 10

Простейшим примером является решение задачи обтекания гладкой непроницаемой пластины изотермическим потоком. При этом  b_т = b = 0, Ψ = 1, и уравнение импульса (3.63) с учетом степенного закона трения будет иметь вид

                        (3.65)

Интегрируя, находим, что

            (3.66)

где индекс «кр.» означает начало развития турбулентного пограничного слоя. Если х_кр = 0, т. е. турбулентный пограничный слой возникает сразу на передней кромке пластины (например, вследствие установки специального турбулизатора), то

                                          (3.67)

и

,                   (3.68)

при  n = 1/7,  m = 0,25,  A = 0,0128  получим

;                                 (3.69)

  или              (3.70)

или с учетом того, что при  n = 1/7   ,

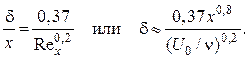                      (3.71)

Как видим, толщина турбулентного пограничного слоя нарастает гораздо интенсивнее, чем ламинарного:

Интегральное соотношение энергии для теплового пограничного  слоя  при  произвольном  изменении  скорости основного потока

U₀ = f₁(x) и для любого закона изменения температуры стенки ΔТ = f₂(x) при течении газа с постоянными физическими свойствами имеет вид

          (3.72)

Его можно привести к виду, более удобному для интегрирования,

                 (3.73)

После интегрирования с учетом начальных условий при х = х₀  получим

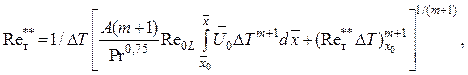   (3.74)

где  – относительная скорость на внешней границе пограничного слоя; – значение этих параметров в сечении х = х₀, начиная с которого ведется расчет (например, – сечение перехода ламинарного течения в турбулентное). В таком случае значение  находится из расчета ламинарного слоя.

Для случая U₀ = const и ΔТ = const, если турбулентный пограничный слой развивается с самого начала (с сечения х = 0), из (3.74)

Подставляя это соотношение в закон теплообмена (3.62), получаем изменение коэффициента теплообмена по длине поверхности:

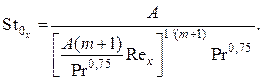                     (3.75)

Для степенного профиля с   n = 1/7, m = 0,25, A = 0,0128

                              (3.76)

Для случая q_ст = const (тепловой поток по длине поверхности не меняется) уравнение энергии

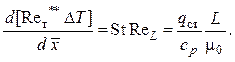                     (3.77)

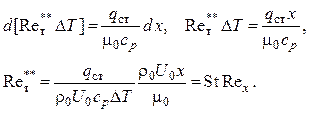                 (3.78)

Подставляя это выражение в степенной закон теплообмена, получаем

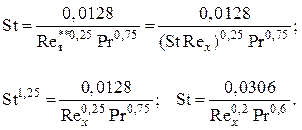                   (3.79)

Отсюда следует, что для любого закона изменения скорости на внешней границе пограничного слоя U₀ = f(x) при расчете теплоотдачи с постоянной тепловой нагрузкой q_ст = const справедлива формула для обтекания плоской пластины, только в числах St и Re_x необходимо подставлять параметры на внешней границе пограничного слоя для рассматриваемого сечения.

Сравнение   формул   (3.79)   и   (3.76)   показывает, что в турбулентном пограничном слое коэффициенты теплоотдачи при условиях T_ст = const  и  q_ст  = const отличаются всего примерно на 6 %, в то время как в ламинарном пограничном слое   [(см. выражение (2.115)]. Это говорит о том, что турбулентный пограничный слой более консервативен к изменению граничных условий, чем ламинарный.